
【题目】把一张矩形纸片ABCD按如图方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.
(1)求证:BH∥DG;
(2)求证:△BEH≌△DFG;
(3)若AB=6 cm,BC=8 cm.
①BF=________cm;
②求线段CG的长.

【答案】(1)见解析;(2)见解析;(3)① 4;②CG=3 cm
【解析】
(1)根据折叠的性质可得![]() ,再根据平行线的性质得到∠1=∠2,故可求解;
,再根据平行线的性质得到∠1=∠2,故可求解;
(2)根据矩形的性质及ASA即可证明△BEH≌△DFG;
(3)①先根据勾股定理求出BD,再得到DF=CD=8,即可求出BF的长;
②由图形翻折变换的性质得出CG=FG,设CG=x,则BG=8x,再利用勾股定理即可求出x的值.
解:(1)由折叠可知:![]() .
.
在矩形ABCD中,AB//CD,
∴∠ABD=∠BDC.
∴∠1=∠2.
∴BH//DG.

(2)在矩形ABCD中,
∴∠A=∠C,AB=CD.
由折叠可知:AB=BE,CD=DF,∠3=∠A,∠4=∠C.
∴BE=DF,∠3=∠4.
在△BEH和△DFG中,

∴△BEH≌△DFG.
(3)①∵四边形ABCD是矩形,AB=6cm,BC=8cm,
∴AB=CD=6cm,AD=BC=8cm,
∴BD=![]()
∵由(2)知,FD=CD,CG=FG,
∴BF=106=4cm,
故答案为:4;
②设CG=x cm,则FG=x cm,BG=(8-x)cm,
在Rt△BGF中,BG2=BF2+FG2,
即![]()
解得x=3
即CG=3 cm.


科目:初中数学 来源: 题型:
【题目】青年志愿者爱心小分队赴山村送温暖,准备为困难村民购买一些米面.已知购买1袋大米、4袋面粉,共需240元;购买2袋大米、1袋面粉,共需165元.
(1)求每袋大米和面粉各多少元?
(2)如果爱心小分队计划购买这些米面共40袋,总费用不超过2140元,那么至少购买多少袋面粉?
查看答案和解析>>
科目:初中数学 来源: 题型:
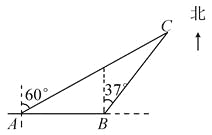
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
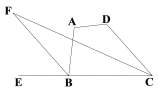
【题目】如图,四边形ABCD的内角∠DCB与外角∠ABE的平分线相交于点F.
(1)若BF∥CD,∠ABC=80°,求∠DCB的度数;
(2)已知四边形ABCD中,∠A=105,∠D=125,求∠F的度数;
(3)猜想∠F、∠A、∠D之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
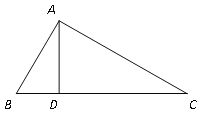
【题目】如图,△ABC中,![]() ,AD是BC边上的高,如果
,AD是BC边上的高,如果![]() ,我们就称△ABC为“高和三角形”.请你依据这一定义回答问题:
,我们就称△ABC为“高和三角形”.请你依据这一定义回答问题:
(1)若![]() ,
,![]() ,则△ABC____ “高和三角形”(填“是”或“不是”);
,则△ABC____ “高和三角形”(填“是”或“不是”);
(2)一般地,如果△ABC是“高和三角形”,则![]() 与
与![]() 之间的关系是____,并证明你的结论
之间的关系是____,并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 的中点,要使四边形
的中点,要使四边形![]() 是矩形,则四边形
是矩形,则四边形![]() 只需要满足一个条件是( )
只需要满足一个条件是( )

A.四边形![]() 是梯形B.四边形
是梯形B.四边形![]() 是菱形
是菱形
C.对角线![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形![]() 中,
中,![]() .射线
.射线![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,同点
的速度运动,同点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,设运动时间为
的速度运动,设运动时间为![]() ;
;

(1)连接![]() ,当
,当![]() 经过
经过![]() 边的中点
边的中点![]() 时,求证:
时,求证:![]() ;
;
(2)求当![]() 为何值,四边形
为何值,四边形![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:_____________,使△AEH≌△CEB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com