
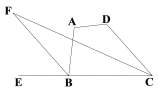
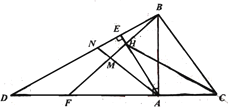
【题目】如图,四边形ABCD的内角∠DCB与外角∠ABE的平分线相交于点F.
(1)若BF∥CD,∠ABC=80°,求∠DCB的度数;
(2)已知四边形ABCD中,∠A=105,∠D=125,求∠F的度数;
(3)猜想∠F、∠A、∠D之间的数量关系,并说明理由.
【答案】(1)50°;(2)25°;(3)∠F=(∠A+∠D-180)°.
【解析】
(1)由∠ABC=80°,可知∠ABE=100°,根据BF平分∠ABE,BF∥CD可得∠BCD=50°.
(2)由三角形外角性质可知∠F=∠FBE-∠FCE,而BF平分∠ABE、CF平分∠BCD,故∠F=![]() (∠ABE-∠FCE),由补角性质和四边形内角和可得∠ABE=360°-∠A-∠B-∠BCD,将已知代入即可求解;
(∠ABE-∠FCE),由补角性质和四边形内角和可得∠ABE=360°-∠A-∠B-∠BCD,将已知代入即可求解;
(3)同(2)可得∠F=![]() (∠A+∠D-180°)
(∠A+∠D-180°)
解:(1)∵∠ABC=80°,
∴∠ABE=180°-∠ABC=100°,
∵BF平分∠ABE,
∴∠EBF=![]() ∠ABE=50°,
∠ABE=50°,
∵BF∥CD
∴∠BCD=∠EBF=50°;
(2)∵∠FBE是△EBC的外角,
∴∠F=∠EBF-∠ECF
∵BF平分∠ABE、CF平分∠BCD,
∴∠EBF=![]() ∠ABE=,∠ECF=
∠ABE=,∠ECF=![]() ∠BCD,
∠BCD,
∵∠ABE=180°-∠ABC,
∴∠F=![]() (180°-∠ABC)-
(180°-∠ABC)-![]() ∠BCD=
∠BCD=![]() [180°-(∠ABC+∠BCD)],
[180°-(∠ABC+∠BCD)],
∵在四边形ABCD中,∠ABC+∠BCD=360°-∠A-∠D,
∴∠F=![]() [180°-(360°-∠A-∠D)],
[180°-(360°-∠A-∠D)],
∴∠F=![]() (∠A+∠D-180°),
(∠A+∠D-180°),
∵∠A=105,∠D=125,
∴∠F=![]() (105 +125 -180°)=25°,
(105 +125 -180°)=25°,
(3)结论:∠F=![]() (∠A+∠D-180°)
(∠A+∠D-180°)
理由如下:∵∠FBE是△EBC的外角,
∴∠F=∠EBF-∠ECF
∵BF平分∠ABE、CF平分∠BCD,
∴∠EBF=![]() ∠ABE=,∠ECF=
∠ABE=,∠ECF=![]() ∠BCD,
∠BCD,
∵∠ABE=180°-∠ABC,
∴∠F=![]() (180°-∠ABC)-
(180°-∠ABC)-![]() ∠BCD=
∠BCD=![]() [180°-(∠ABC+∠BCD)],
[180°-(∠ABC+∠BCD)],
∵在四边形ABCD中,∠ABC+∠BCD=360°-∠A-∠D,
∴∠F=![]() [180°-(360°-∠A-∠D)],
[180°-(360°-∠A-∠D)],
∴∠F=![]() (∠A+∠D-180°),
(∠A+∠D-180°),


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
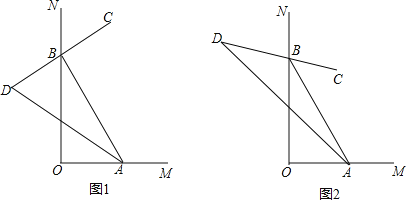
【题目】如图,∠MON=90°,点A、B分别在OM、ON上运动(不与点O重合).
(1)如图①,BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交于点D.
①若∠BAO=60°,则∠D的大小为 度,
②猜想:∠D的度数是否随A、B的移动发生变化?请说明理由.
(2)如图②,若∠ABC=![]() ∠ABN, ∠BAD=
∠ABN, ∠BAD=![]() ∠BAO,则∠D的大小为 度,若∠ABC=
∠BAO,则∠D的大小为 度,若∠ABC=![]() ∠ABN, ∠BAD=
∠ABN, ∠BAD=![]() ∠BAO,则∠D的大小为 度(用含n的代数式表示).
∠BAO,则∠D的大小为 度(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
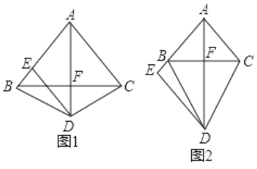
【题目】如图1,已知△ABC中,AB=AC,点D是△ABC外一点(与点A分别在直线BC两侧).且DB=DC,过点D作DE//AC,交射线AB于E,连接AD交BC于F.
(1)求证:AD垂直BC;
(2)如图1,点E在线段AB上且不与B重合时,求证:DE=AE;
(3)如图2,当点E在线段AB的延长线上时,请直接写出线段DE,AC,BE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中的对角线AC,BD相交于O,EF过点O,与AD,BC分别相交于点E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长为( )
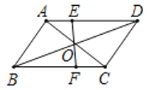
A.10B.11C.12D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
学习了无理数、二次根式及完全平方公式后,某数学兴趣小组开展了一次探究活动:
估算![]() 的近似值.
的近似值.
小明的方法:
∵![]() ,
,
设![]() (0<k<1),
(0<k<1),
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() .
.
(1)请你用小明的方法估算![]() 的近似值(结果保留两位小数);
的近似值(结果保留两位小数);
(2)请你结合上述实例,概括出估算![]() 的公式:已知非负整数a,b,m,若
的公式:已知非负整数a,b,m,若![]() ,且
,且![]() ,则
,则![]() =_____________(用含a,b的代数式表示)
=_____________(用含a,b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张矩形纸片ABCD按如图方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.
(1)求证:BH∥DG;
(2)求证:△BEH≌△DFG;
(3)若AB=6 cm,BC=8 cm.
①BF=________cm;
②求线段CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+8与x轴、y轴分别交于A.B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
x+8与x轴、y轴分别交于A.B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )

A. (0,4) B. (0,3) C. (﹣4,0) D. (0,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() 、
、![]() 为直线
为直线![]() 上两点,且满足
上两点,且满足![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)若点![]() 是线段
是线段![]() 上的动点,连
上的动点,连![]() 并延长交
并延长交![]() 于
于![]() ,当
,当![]() 在线段
在线段![]() 的什么位置上时,
的什么位置上时,![]() ?请说明理由;
?请说明理由;
(3)在(2)的结论下,判断线段![]() 、
、![]() 、
、![]() 的数量关系.请说明理由.
的数量关系.请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com