
【题目】阅读材料:
学习了无理数、二次根式及完全平方公式后,某数学兴趣小组开展了一次探究活动:
估算![]() 的近似值.
的近似值.
小明的方法:
∵![]() ,
,
设![]() (0<k<1),
(0<k<1),
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() .
.
(1)请你用小明的方法估算![]() 的近似值(结果保留两位小数);
的近似值(结果保留两位小数);
(2)请你结合上述实例,概括出估算![]() 的公式:已知非负整数a,b,m,若
的公式:已知非负整数a,b,m,若![]() ,且
,且![]() ,则
,则![]() =_____________(用含a,b的代数式表示)
=_____________(用含a,b的代数式表示)
科目:初中数学 来源: 题型:
【题目】某校七年级有400名学生,其中2004年出生的有8人,2005年出生的有292人,2006年出生的有75人,其余的为2007年出生.
(1)该年级至少有两人同月同日生,这是一个 事件(填“必然”、“不可能”或“随机”);
(2)从这400名学生中随机选一人,选到2007年出生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下列要求画图(不需书写结论)并填空;如右图,
(1)过点Q作QD⊥AB,垂足为D,
(2)过点Q作QE∥AB,交AC于点E,
(3)过点Q作QF⊥直线 AC,垂足为F,
(4)联结A、Q两点,
(5)点Q到直线AC的距离是线段 的长度,
(6)直线QE与直线AB之间的距离是线段 的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
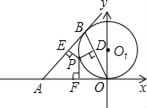
【题目】如图,OB是以(O,a)为圆心,a为半径的⊙O1的弦,过B点作⊙O1的切线,P为劣弧![]() 上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.
上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.
(1)求证:PD2=PEPF;
(2)当∠BOP=30°,P点为OB的中点时,求D、E、F、P四个点的坐标及S△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
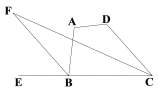
【题目】如图,四边形ABCD的内角∠DCB与外角∠ABE的平分线相交于点F.
(1)若BF∥CD,∠ABC=80°,求∠DCB的度数;
(2)已知四边形ABCD中,∠A=105,∠D=125,求∠F的度数;
(3)猜想∠F、∠A、∠D之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.

(1)学校采用的调查方式是 ;学校共选取了 名学生;
(2)补全统计图中的数据:条形统计图中羽毛球 人、乒乓球 人、其他 人、扇形统计图中其他 %;
(3)该校共有1200名学生,请估计喜欢“乒乓球”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 的中点,要使四边形
的中点,要使四边形![]() 是矩形,则四边形
是矩形,则四边形![]() 只需要满足一个条件是( )
只需要满足一个条件是( )

A.四边形![]() 是梯形B.四边形
是梯形B.四边形![]() 是菱形
是菱形
C.对角线![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD
面上的概率为0.75;若存在,指出其中的一种平移方式;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com