
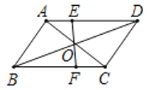
【题目】如图,平行四边形ABCD中的对角线AC,BD相交于O,EF过点O,与AD,BC分别相交于点E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长为( )
A.10B.11C.12D.13
【答案】C
【解析】
根据平行四边形的对边相等得:CD=AB=4,AD=BC=5.再根据平行四边形的性质和对顶角相等可以证明:△AOE≌△COF.根据全等三角形的性质,得:OF=OE=1.5,CF=AE,故四边形EFCD的周长为CD+EF+AD=12.
∵四边形ABCD是平行四边形,
∴CD=AB=4,AD=BC=5,OA=OC,AD∥BC,
∴∠EAO=∠FCO,∠AEO=∠CFO,
在△AOE和△COF中,
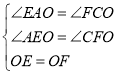 ,
,
∴△AOE≌△COF(AAS),
∴OF=OE=1.5,CF=AE,
故四边形EFCD的周长为CD+EF+ED+FC=CD+EF+AE+ED=CD+AD+EF=4+5+1.5×2=12.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠BAD, ∠ACD=∠ABC=90°,E、F分别为AC、CD的中点,∠D=62°,则∠BEF的度数为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
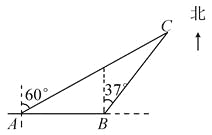
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的内角∠DCB与外角∠ABE的平分线相交于点F.
(1)若BF∥CD,∠ABC=80°,求∠DCB的度数;
(2)已知四边形ABCD中,∠A=105,∠D=125,求∠F的度数;
(3)猜想∠F、∠A、∠D之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
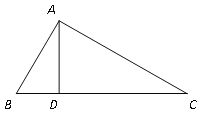
【题目】如图,△ABC中,![]() ,AD是BC边上的高,如果
,AD是BC边上的高,如果![]() ,我们就称△ABC为“高和三角形”.请你依据这一定义回答问题:
,我们就称△ABC为“高和三角形”.请你依据这一定义回答问题:
(1)若![]() ,
,![]() ,则△ABC____ “高和三角形”(填“是”或“不是”);
,则△ABC____ “高和三角形”(填“是”或“不是”);
(2)一般地,如果△ABC是“高和三角形”,则![]() 与
与![]() 之间的关系是____,并证明你的结论
之间的关系是____,并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形![]() 中,
中,![]() .射线
.射线![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,同点
的速度运动,同点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,设运动时间为
的速度运动,设运动时间为![]() ;
;

(1)连接![]() ,当
,当![]() 经过
经过![]() 边的中点
边的中点![]() 时,求证:
时,求证:![]() ;
;
(2)求当![]() 为何值,四边形
为何值,四边形![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=115°,那么∠BFD的度数是
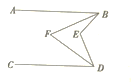
A.62°B.64°C.57.5°D.60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com