
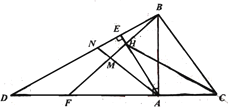
【题目】如图,已知![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() 、
、![]() 为直线
为直线![]() 上两点,且满足
上两点,且满足![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)若点![]() 是线段
是线段![]() 上的动点,连
上的动点,连![]() 并延长交
并延长交![]() 于
于![]() ,当
,当![]() 在线段
在线段![]() 的什么位置上时,
的什么位置上时,![]() ?请说明理由;
?请说明理由;
(3)在(2)的结论下,判断线段![]() 、
、![]() 、
、![]() 的数量关系.请说明理由.
的数量关系.请说明理由.
 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
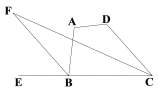
【题目】如图,四边形ABCD的内角∠DCB与外角∠ABE的平分线相交于点F.
(1)若BF∥CD,∠ABC=80°,求∠DCB的度数;
(2)已知四边形ABCD中,∠A=105,∠D=125,求∠F的度数;
(3)猜想∠F、∠A、∠D之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:_____________,使△AEH≌△CEB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A、D),Q是BC边上的任意一点. 连AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.

(1)求证:△APE∽△ADQ;
(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?
(3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=115°,那么∠BFD的度数是
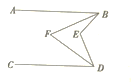
A.62°B.64°C.57.5°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
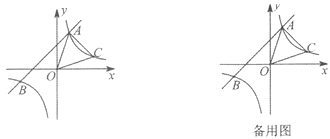
【题目】已知:如图,一次函数y=x+2的图象与反比例函数y=![]() 的图象交于A、B两点,且点A的坐标为(1,m).
的图象交于A、B两点,且点A的坐标为(1,m).
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)点C(n,1)在反比例函数y=![]() 的图象上,求△AOC的面积.
的图象上,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=3,b=4,c=5; ②a=6,∠A=45°;③a=2,b=2,c=2![]() ; ④∠A=38°,∠B=52°.
; ④∠A=38°,∠B=52°.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com