练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一次函数y=kx+b的图象经过A、B两点，与x轴交于点C，则此一次函数的解析式为__________，△AOC的面积为_________．

    【答案】y=x+2 4

    【解析】

    一次函数y=kx+b的图象经过A、B两点，即A（2，4），B（0，2），代入可求出函数关系式．再根据三角形的面积公式，得出△AOC的面积．

    解：一次函数y=kx+b的图象经过A、B两点，即A（2，4），B（0，2），

    与x轴交于点C（-2，0），

    根据一次函数解析式的特点，可得出方程组，解得

    则此一次函数的解析式为y=x+2，

    △AOC的面积=|-2|×4÷2=4．

    则此一次函数的解析式为y=x+2，△AOC的面积为4．

    故答案为：y=x+2；4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形中，、、、分别是、、、的中点，要使四边形是矩形，则四边形只需要满足一个条件是（ ）

    A.四边形是梯形B.四边形是菱形

    C.对角线D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于A、D），Q是BC边上的任意一点. 连AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F.

    （1）求证：△APE∽△ADQ；

    （2）设AP的长为x，试求△PEF的面积S△PEF关于x的函数关系式，并求当P在何处时，S△PEF取得最大值？最大值为多少？

    （3）当Q在何处时，△ADQ的周长最小？（须给出确定Q在何处的过程或方法，不必给出证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为美化校园，计划对面积为1800m2的区域进行绿化，安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400 m2区域的绿化时，甲队比乙队少用4天.

    （1）求甲、乙两工程队每天能完成绿化的面积分别是多少m2？

    （2）若学校每天需付给甲队的绿化费用是0.4万元，乙队为0.25万元，要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的弦，D为OA半径的中点，过D作CD⊥OA交弦AB于点E，交⊙O于点F，且CE=CB．

    （1）求证：BC是⊙O的切线；

    （2）连接AF、BF，求∠ABF的度数；

    （3）如果BE=10，sinA=，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y，的对应值如下表：

    x

    …

    -2

    -1

    0

    1

    2

    …

    y

    …

    0

    -4

    -4

    0

    8

    …

    （1）根据上表填空：

    ①抛物线与x轴的交点坐标是_________和_________；

    ②抛物线经过点（-3，_________）；

    （2）试确定抛物线y=ax2+bx+c的解析式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

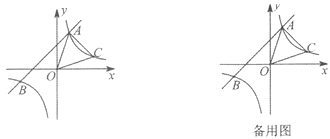
    【题目】已知：如图，一次函数y=x+2的图象与反比例函数y=的图象交于A、B两点，且点A的坐标为（1，m）.

    （1）求反比例函数y=的表达式；

    （2）点C（n，1）在反比例函数y=的图象上，求△AOC的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中学生骑电动车上学给交通安全带来隐患，为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度，从中随机调查400个家长，结果有360个家长持反对态度，则下列说法正确的是( )

    A. 调查方式是普查 B. 该校只有360个家长持反对态度

    C. 样本是360个家长 D. 该校约有90%的家长持反对态度

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=x2﹣x﹣9与x轴交于A、B两点，与y轴交于点C，连接BC、AC．

    （1）求AB和OC的长；

    （2）点E从点A出发，沿x轴向点B运动（点E与点A、B不重合），过点E作直线l平行BC，交AC于点D．设AE的长为m，△ADE的面积为s，求s关于m的函数关系式，并写出自变量m的取值范围；

    （3）在（2）的条件下，连接CE，求△CDE面积的最大值；此时，求出以点E为圆心，与BC相切的圆的面积（结果保留π）．

    查看答案和解析>>

    同步练习册答案