
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=![]() x2Љ
x2Љ![]() xЉ9гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌСЌНгBCЁЂACЃЎ
xЉ9гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌСЌНгBCЁЂACЃЎ
ЃЈ1ЃЉЧѓABКЭOCЕФГЄЃЛ
ЃЈ2ЃЉЕуEДгЕуAГіЗЂЃЌбиxжсЯђЕуBдЫЖЏЃЈЕуEгыЕуAЁЂBВЛжиКЯЃЉЃЌЙ§ЕуEзїжБЯпlЦНааBCЃЌНЛACгкЕуDЃЎЩшAEЕФГЄЮЊmЃЌЁїADEЕФУцЛ§ЮЊsЃЌЧѓsЙигкmЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНгCEЃЌЧѓЁїCDEУцЛ§ЕФзюДѓжЕЃЛДЫЪБЃЌЧѓГівдЕуEЮЊдВаФЃЌгыBCЯрЧаЕФдВЕФУцЛ§ЃЈНсЙћБЃСєІаЃЉЃЎ

ЁОД№АИЁПЃЈ1ЃЉAB=9ЃЌOC=9ЃЛЃЈ2ЃЉs=![]() m2ЃЈ0ЃМmЃМ9ЃЉЃЛЃЈ3ЃЉ
m2ЃЈ0ЃМmЃМ9ЃЉЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉвбжЊХзЮяЯпЕФНтЮіЪНЃЌЕБ![]() ПЩШЗЖЈ
ПЩШЗЖЈ![]() ЕузјБъЃЛЕБ
ЕузјБъЃЛЕБ![]() ЪБЃЌПЩШЗЖЈ
ЪБЃЌПЩШЗЖЈ![]() ЕуЕФзјБъЃЌНјЖјШЗЖЈ
ЕуЕФзјБъЃЌНјЖјШЗЖЈ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ЃЈ2ЃЉжБЯп![]() ПЩЕУГі
ПЩЕУГі![]() ЯрЫЦЃЌЫќУЧЕФУцЛ§БШЕШгкЯрЫЦБШЕФЦНЗНЃЌгЩДЫЕУЕНЙигк
ЯрЫЦЃЌЫќУЧЕФУцЛ§БШЕШгкЯрЫЦБШЕФЦНЗНЃЌгЩДЫЕУЕНЙигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЛИљОнЬтИЩЬѕМўЃКЕу
ЕФКЏЪ§ЙиЯЕЪНЃЛИљОнЬтИЩЬѕМўЃКЕу![]() гыЕу
гыЕу![]() ВЛжиКЯЃЌПЩШЗЖЈ
ВЛжиКЯЃЌПЩШЗЖЈ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉЂйЪзЯШгУ![]() СаГі
СаГі![]() ЕФУцЛ§БэДяЪНЃЌ
ЕФУцЛ§БэДяЪНЃЌ ![]() ЕФУцЛ§ВюМДЮЊ
ЕФУцЛ§ВюМДЮЊ![]() ЕФУцЛ§ЃЌгЩДЫПЩЕУЙигк
ЕФУцЛ§ЃЌгЩДЫПЩЕУЙигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЌИљОнКЏЪ§ЕФаджЪПЩЕУЕН
ЕФКЏЪ§ЙиЯЕЪНЃЌИљОнКЏЪ§ЕФаджЪПЩЕУЕН![]() ЕФзюДѓУцЛ§вдМАДЫЪБ
ЕФзюДѓУцЛ§вдМАДЫЪБ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкЙ§![]() зі
зі![]() ЕФДЙЯп
ЕФДЙЯп![]() ЃЌетИіДЙЯпЖЮЕФГЄМДЮЊгы
ЃЌетИіДЙЯпЖЮЕФГЄМДЮЊгы![]() ЯрЧаЕФ
ЯрЧаЕФ![]() ЕФАыОЖЃЌПЩИљОнЯрЫЦШ§НЧаЮ
ЕФАыОЖЃЌПЩИљОнЯрЫЦШ§НЧаЮ![]() ЕУЕНЕФЯрЙиБШР§ЯпЖЮЧѓЕУИУАыОЖЕФжЕЃЌгЩДЫЕУНтЃЎ
ЕУЕНЕФЯрЙиБШР§ЯпЖЮЧѓЕУИУАыОЖЕФжЕЃЌгЩДЫЕУНтЃЎ
ЪдЬтНтЮіЃК(1)вбжЊЃКХзЮяЯп![]()
ЕБx=0ЪБ,y=9,дђЃКC(0,9)ЃЛ
ЕБy=0ЪБ, ![]() ,ЕУЃК
,ЕУЃК ![]() ,дђЃКA(3,0)ЁЂB(6,0)ЃЛ
,дђЃКA(3,0)ЁЂB(6,0)ЃЛ
ЁрAB=9ЃЌOC=9.
(2) ![]()
ЁрЁїAEDЁзЁїABCЃЌ
 МДЃК
МДЃК 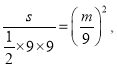 ЕУЃК
ЕУЃК ![]()

(3)НтЗЈвЛЃК ![]()
![]()
Ёп0<m<9ЃЌ
ЁрЕБ![]() ЪБ,
ЪБ, ![]() ШЁЕУзюДѓжЕ,зюДѓжЕЮЊ
ШЁЕУзюДѓжЕ,зюДѓжЕЮЊ![]() ДЫЪБ,
ДЫЪБ, ![]()
МЧEгыBCЯрЧагкЕуMЃЌСЌНгEMЃЌдђEMЁЭBCЃЌЩшEЕФАыОЖЮЊr.
дк![]() жа,
жа, ![]()
![]()
ЁрЁїBOCЁзЁїBMEЃЌ
![]()

![]()
ЁрЫљЧѓ![]() ЕФУцЛ§ЮЊЃК
ЕФУцЛ§ЮЊЃК 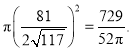


 УћЬтН№ОэЯЕСаД№АИ
УћЬтН№ОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=kx+bЕФЭМЯѓОЙ§AЁЂBСНЕуЃЌгыxжсНЛгкЕуCЃЌдђДЫвЛДЮКЏЪ§ЕФНтЮіЪНЮЊ__________ЃЌЁїAOCЕФУцЛ§ЮЊ_________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаЮхеХе§УцЗжБ№БъгаЪ§зжЉ2ЃЌЉ1ЃЌ0ЃЌ1ЃЌ2ЕФПЈЦЌЃЌЫќУЧГ§Ъ§зжВЛЭЌЭтЦфгрШЋВПЯрЭЌЃЎЯжНЋЫќУЧБГУцГЏЩЯЃЌЯДдШКѓДгжаЫцЛњГщШЁвЛеХЃЌМЧПЈЦЌЩЯЕФЪ§зжЮЊaЃЌдђЪЙЙигкxЕФвЛдЊЖўДЮЗНГЬx2Љ2ЃЈaЉ1ЃЉx+aЃЈaЉ3ЃЉ=0гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧввдxЮЊздБфСПЕФЖўДЮКЏЪ§y=x2ЉЃЈa2+1ЃЉxЉa+2ЕФЭМЯѓВЛОЙ§ЕуЃЈ1ЃЌ0ЃЉЕФИХТЪЪЧ__ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌЯШАбвЛОиаЮ![]() жНЦЌЩЯЯТЖделЃЌЩшелКлЮЊ
жНЦЌЩЯЯТЖделЃЌЩшелКлЮЊ![]() ЃЛШчЭМЂкЃЌдйАб
ЃЛШчЭМЂкЃЌдйАб
Еу![]() ЕўдкелКлЯп
ЕўдкелКлЯп![]() ЩЯЃЌЕУЕН
ЩЯЃЌЕУЕН![]()
![]() ЃЎЙ§
ЃЎЙ§![]() Еузї
Еузї![]() ЃЌЗжБ№НЛ
ЃЌЗжБ№НЛ![]() ЁЂ
ЁЂ![]() гкЕу
гкЕу![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК ![]() Ёз
Ёз![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЭМЂкжаЃЌШчЙћбижБЯп![]() дйДЮелЕўжНЦЌЃЌЕу
дйДЮелЕўжНЦЌЃЌЕу![]() ФмЗёЕўдкжБЯп
ФмЗёЕўдкжБЯп![]() ЩЯЃПЧыЫЕУїРэгЩЃЛ
ЩЯЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЖШЃЎ
ЕФГЄЖШЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧзївЛИіНЧЕФНЧЦНЗжЯпЕФЗНЗЈЃКвд![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЮЊдВаФЃЌвдШЮвтГЄЮЊАыОЖЛЛЁЃЌЗжБ№НЛ
ЮЊдВаФЃЌвдШЮвтГЄЮЊАыОЖЛЛЁЃЌЗжБ№НЛ![]() гк
гк![]() СНЕуЃЌдйЗжБ№вд
СНЕуЃЌдйЗжБ№вд![]() ЮЊдВаФЃЌДѓгк
ЮЊдВаФЃЌДѓгк![]() ГЄЮЊАыОЖзїЛЛЁЃЌСНЬѕЛЁНЛгкЕу
ГЄЮЊАыОЖзїЛЛЁЃЌСНЬѕЛЁНЛгкЕу![]() ЃЌзїЩфЯп
ЃЌзїЩфЯп![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .
.

ЃЈ1ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШє![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌEЃЌFЃЌGЃЌHЗжБ№ЪЧБпABЃЌBCЃЌCDЃЌDAЕФжаЕуЃЎ
(1)ХаЖЯЫФБпаЮEFGHЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЛ
(2)ЕБBDЃЌACТњзуЪВУДЬѕМўЪБЃЌЫФБпаЮEFGHЪЧе§ЗНаЮЃЎ(ВЛвЊЧѓжЄУї)

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() дк
дк![]() ЕФжБОЖ
ЕФжБОЖ![]() ЕФбгГЄЯпЩЯЃЌЕу
ЕФбгГЄЯпЩЯЃЌЕу![]() дк
дк![]() ЩЯЃЌ
ЩЯЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ

ЃЈ1ЃЉЧѓжЄЃК ![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЕФАыОЖЮЊ2ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§.
ЕФАыОЖЮЊ2ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЮЊСЫВтСПФГНЈжўЮяCDЕФИпЖШЃЌЯШдкЕиУцЩЯгУВтНЧвЧздAДІВтЕУНЈжўЮяЖЅВПЕФбіНЧЪЧ30ЁуЃЌШЛКѓдкЫЎЦНЕиУцЩЯЯђНЈжўЮяЧАНјСЫ100 mЃЌДЫЪБздBДІВтЕУНЈжўЮяЖЅВПЕФбіВПНЧЪЧ45ЁуЃЎвбжЊВтНЧвЧЕФИпЖШЪЧ1ЃЎ5 mЃЌЧыФуМЦЫуГіИУНЈжўЮяЕФИпЖШЃЎЃЈШЁЁж1ЃЎ732ЃЌНсЙћОЋШЗЕН1 mЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФужЊЕРЪ§бЇжаЕФећЬхЫМЯыТ№?НтЬтжаЃЌШєАбзЂвтСІКЭзХблЕуЗХдкЮЪЬтЕФећЬхЩЯЃЌЖрЗНЮЛЫМПМЁЂСЊЯыЁЂЬНОПЃЌНјааећЬхЫМПМЁЂећЬхМгМѕЃЌФмЪЙЮЪЬтбИЫйЛёНт.
Р§ЬтЃКвбжЊx2+xy=4ЃЌxy+y2=-1.ЧѓДњЪ§ЪНx2-y2ЕФжЕ.
НтЃКНЋСНЪНЯрМѕЃЌЕУ(x2+xy)-(xy+y2)=4-(-1)ЃЌМДx2-y2=5ЃЛЧыгУећЬхЫМЯыНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉдкР§ЬтЕФЛљДЁЩЯЧѓ(x+y)2ЕФжЕЃЛ
ЃЈ2ЃЉШєЙигкxЁЂyЕФЖўдЊвЛДЮЗНГЬзщ![]() ЕФНтвВЪЧЖўдЊвЛДЮЗНГЬx+y=6ЕФНтЃЌЧѓkЕФжЕ.
ЕФНтвВЪЧЖўдЊвЛДЮЗНГЬx+y=6ЕФНтЃЌЧѓkЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com