
【题目】已知一次函数y=x+4的图象与二次函数y=ax(x﹣2)的图象相交于A(﹣1,b)和B,点P是线段AB上的动点(不与A、B重合),过点P作PC⊥x轴,与二次函数y=ax(x﹣2)的图象交于点C.
(1)求a、b的值
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,请直接写出点P的坐标.
【答案】
(1)解:∵A(﹣1,b)在直线y=x+4上,
∴b=﹣1+4=3,
∴A(﹣1,3).
又∵A(﹣1,3)在抛物线y=ax(x﹣2)上,
∴3=﹣a(﹣1﹣2),
解得:a=1.
(2)解:设P(m,m+4),则C(m,m2﹣2m).
∴PC=(m+4)﹣(m2﹣2m)
=﹣m2+3m+4
=﹣(m﹣ ![]() )2+
)2+ ![]() ,
,
∵(m﹣ ![]() )2≥0,
)2≥0,
∴﹣(m﹣ ![]() )2+
)2+ ![]() ≤
≤ ![]() .
.
∴当m= ![]() 时,PC有最大值,最大值为
时,PC有最大值,最大值为 ![]() .
.
(3)解:如图
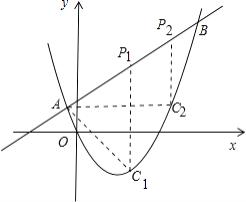 ,
,
P(m,m+4),C(m,m2﹣2m),
AP2=(m+1)2+(m+4﹣3)2=2(m+1)2,AC2=(m+1)2+(m2﹣2m﹣3)2,PC2=(﹣m2+3m+4)2.
①当AP2+AC2=PC2时,即2(m+1)2+(m+1)2+(m2﹣2m﹣3)2=(﹣m2+3m+4)2,
3(m+1)2+[(m2﹣2m﹣3)2﹣(﹣m2+3m+4)2]=0
化简,得(m+1)(m+1)(m﹣2)=0,
解得m=﹣1(不符合题意,舍),m=2,
当m=2时,m+4=6,即P(2,6);
②当AP2=AC2+PC2时,即2(m+1)2=(m+1)2+(m2﹣2m﹣3)2+(﹣m2+3m+4)2,
化简,得
(m﹣4)(m+1)(m+1)(m﹣3)=0.
解得m=4(不符合题意,舍),m=﹣1(不符合题意,舍),m=3,
当m=3时,m+4=7,
即(3,7),
综上所述:若△PAC为直角三角形,点P的坐标为P1(2,6),P2(3,7).
【解析】(1)由A(﹣1,b)在直线y=x+4上,求出b的值,得到A点坐标,再代入二次函数的解析式,求出a的值;(2)由点P在一次函数y=x+4的图象上得到P点的坐标与C点坐标的代数式,根据两点间的距离公式得到PC的最大值;(3)由(2)中的P、C点坐标的代数式,再根据勾股定理求出m的值,求出若△PAC为直角三角形,点P的坐标;此题是综合题,难度较大,计算和解方程时需认真仔细.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于 ![]() 的一元二次方程
的一元二次方程 ![]() 的两个根,且OA>OB
的两个根,且OA>OB
(1)求cos∠ABC的值。
(2)若E为x轴上的点,且 ![]() ,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由
,求出点E的坐标,并判断△AOE与△DAO是否相似?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七![]() 班共有45人,该班计划为每名学生购买一套学具,超市现有A、B两种品牌学具可供选择
班共有45人,该班计划为每名学生购买一套学具,超市现有A、B两种品牌学具可供选择![]() 已知1套A学具和1套B学具的售价为45元;2套A学具和5套B学具的售价为150元.
已知1套A学具和1套B学具的售价为45元;2套A学具和5套B学具的售价为150元.
![]() 、B两种学具每套的售价分别是多少元?
、B两种学具每套的售价分别是多少元?
![]() 现在商店规定,若一次性购买A型学具超过20套,则超出部分按原价的6折出售
现在商店规定,若一次性购买A型学具超过20套,则超出部分按原价的6折出售![]() 设购买A型学具a套
设购买A型学具a套![]() 且不超过30套,购买A、B两种型号的学具共花费w元.
且不超过30套,购买A、B两种型号的学具共花费w元.
![]() 请写出w与a的函数关系式;
请写出w与a的函数关系式;
![]() 请帮忙设计最省钱的购买方案,并求出所需费用.
请帮忙设计最省钱的购买方案,并求出所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买![]() 个甲种文具、
个甲种文具、![]() 个乙种文具共需花费
个乙种文具共需花费![]() 元;购买
元;购买![]() 个甲种文具、
个甲种文具、![]() 个乙种文具共需花费
个乙种文具共需花费![]() 元.
元.
(1)求购买一个甲种文具、一个乙种文具各需多少元?
(2)若学校计划购买这两种文具共![]() 个,投入资金不少于
个,投入资金不少于![]() 元又不多于
元又不多于![]() 元,设购买甲种文具
元,设购买甲种文具![]() 个,求有多少种购买方案?
个,求有多少种购买方案?
(3)设学校投入资金![]() 元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列推理过程
已知:∠C+∠CBD=180°,∠ABD=85°,∠2=60°,求∠A的度数.

解:∵∠C+∠CBD=180°(已知)
∴DB∥CE( )
∴∠1= ( )
∵∠2=∠3( )
∴∠1=∠2=60° ( )
又∵ ∠ABD=85°(已知)
∴∠A=180°-∠ABD-∠1= (三角形三内角和为180°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1,2,3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.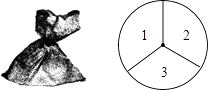
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车开往距离出发地![]() 的目的地,出发后第一个小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前
的目的地,出发后第一个小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前![]() 到达目的地,设第一个小时内行驶的速度为
到达目的地,设第一个小时内行驶的速度为![]() .
.
(1)求汽车实际走完全程所花的时间
(2)若按原路返回,司机准备一半路程以![]() 的速度行驶,另一半路程以
的速度行驶,另一半路程以![]() 的速度行驶
的速度行驶![]() ,朋友建议他一半时间以
,朋友建议他一半时间以![]() 的速度行驶,另一半时间以
的速度行驶,另一半时间以![]() 的速度行驶,你觉得谁的方案会更快?请说明理由.
的速度行驶,你觉得谁的方案会更快?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com