

分析 (1)过点D作DM⊥直线l交CA的延长线于点M,根据平行线的性质结合等腰直角三角形的性质可得出∠AMD=45°=∠ECD,CD=MD.再通过角的计算得出∠EDC=∠ADM,由此即可证出△ADM≌△EDC,从而得出DA=DE;
(2)过点D直线l的垂线,交AC于点F,通过角的计算以及等腰直角三角形的性质即可证得△CDE≌△FDA,由此即可得出结论DA=DE;
(3)分两种情况考虑:①点D在点C的右侧时,如同(1)过点A作AN⊥DM于点N,通过解直角三角形即可求出AM的长度,根据全等三角形的性质即可得出结论;②当点D在C点的右侧时,过点A作AN⊥DM于点N,结合(1)(2)的结论以及等腰直角三角形的性质即可求出线段CN个NE的长度,二者相加即可得出结论.
解答 解:(1)过点D作DM⊥直线l交CA的延长线于点M,如图1所示.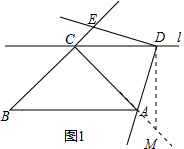 ∵△ABC为等腰直角三角形,∠ACB=90°,AC=BC,
∵△ABC为等腰直角三角形,∠ACB=90°,AC=BC,
∴∠ABC=∠BAC=45°.
∵直线l∥AB,
∴∠ECD=∠ABC=45°,∠ACD=∠BAC=45°,
∵DM⊥直线l,
∴∠CDM=90°,
∴∠AMD=45°=∠ECD,CD=MD.
∵∠EDC+∠CDA=90°,∠CDA+∠ADM=90°,
∴∠EDC=∠ADM.
在△ADM和△EDC中,有$\left\{\begin{array}{l}{∠EDC=∠ADM}\\{CD=MD}\\{∠ECD=∠AMD}\end{array}\right.$,
∴△ADM≌△EDC(ASA),
∴DA=DE.
(2)证明:过点D直线l的垂线,交AC于点F,如图2所示.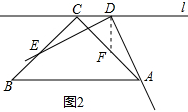
∵△ABC中,∠BCA=90°,AC=BC,
∴∠CAB=∠B=45°.
∵直线l∥AB,
∴∠DCF=∠CAB=45°.
∵FD⊥直线l,
∴∠DCF=∠DFC=45°.
∴CD=FD.
∵∠DFA=180°-∠DFC=135°,∠DCE=∠DCA+∠BCA=135°,
∴∠DCE=∠DFA.
∵∠CDE+∠EDF=90°,∠EDF+∠FDA=90°,
∴∠CDE=∠FDA.
在△CDE和△FDA中,有$\left\{\begin{array}{l}{∠DCE=∠DFA}\\{CD=FD}\\{∠CDE=∠FDA}\end{array}\right.$,
∴△CDE≌△FDA(ASA),
∴DE=DA.
(3)CD=$2\sqrt{2}$分两种情况:
①当点D在C点的右侧时,过点A作AN⊥DM于点N,如图3所示. ∵△ADM≌△EDC,
∵△ADM≌△EDC,
∴DM=DC=$2\sqrt{2}$,CE=AM,
∵AC=3,
∴DN=$\frac{\sqrt{2}}{2}$AC=$\frac{3\sqrt{2}}{2}$,
∴NM=DM-DN=$\frac{\sqrt{2}}{2}$,
∴AM=CE=$\sqrt{2}$NM=1;
②当点D在C点的左侧时,过点A作AA′⊥直线l于点A′,过点D作DN⊥直线L交CB的延长线与点N,过点E作EM⊥DM于点M,如图4所示.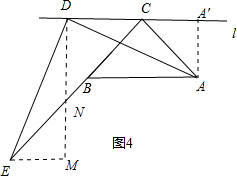 ∵∠A′DA+∠ADM=90°,∠ADM+∠MDE=90°,
∵∠A′DA+∠ADM=90°,∠ADM+∠MDE=90°,
∴∠A′DA=∠MDE,
在△A′DA和△MDE中,有$\left\{\begin{array}{l}{A′D=MD}\\{∠A′DA=∠MDE}\\{AD=ED}\end{array}\right.$,
∴△A′DA≌△MDE(SAS),
∴AA′=EM.
∵∠CAA′=45°,AC=3,
∴AA′=$\frac{3\sqrt{2}}{2}$.
∵∠DCN=45°,CD=2$\sqrt{2}$,
∴CN=4.
∵∠NEM=45°,EM=AA′=$\frac{3\sqrt{2}}{2}$,
∴NE=3.
∴CE=CN+NE=4+3=7,
综上可知:CE的长为1或7.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定及性质以及解直角三角形,解题的关键是:(1)证出△ADM≌△EDC;(2)证出△CDE≌△FDA;(3)分点D在点C的左、右两侧考虑.本题属于难题,(1)(2)难度不大,解决第三小问时,用到前两问的结论,分点D在点C的左、右两侧考虑,在解决该问时,巧妙地利用等腰直角三角形的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
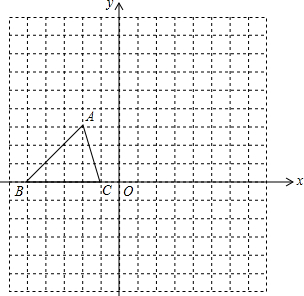 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差 | 0.56 | 0.60 | 0.50 | 0.45 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知直线AB、CD相交于点O,OB平分∠EOD,若∠EOD=110°,则∠AOC的度数是( )
如图,已知直线AB、CD相交于点O,OB平分∠EOD,若∠EOD=110°,则∠AOC的度数是( )| A. | 35° | B. | 55° | C. | 70° | D. | 110° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com