
【题目】有一副直角三角板按如图所示放置,点E、F分别在线段AB和线段AC上,∠DEF=∠BAC=90°,∠D=45°,∠C=30°.
(1)若∠DEA=28°,求∠DFA的度数.
(2)当∠DFC等于多少度时,EF∥BC?说说你的理由.
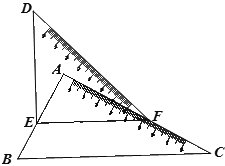
【答案】(1)∠DFA= 17°;(2)∠DFC=165°时EF∥BC.
【解析】
(1)先求出∠AEF的度数,继而在△AEF中,求出∠AFE的度数,结合∠DFE=45°,即可求得答案;
(2)当∠DFC=165°时EF∥BC,理由如下:由平角义可求得∠DFA=15°,再由∠DFE=45°,可求得∠AFE=30°,继而根据∠C=30°,可得∠AFE=∠C,根据同位角相等,两直线平行,即可求得EF//BC.
(1)∵∠DEF=90°,∠DEA=28°,
∴∠AEF=∠DEF-∠DEA=90°-28°=62°,
在△AEF中,∠A=90°,∴∠AFE=90°-∠AEF=90°-62°=28°,
∵∠DFE=45°,∴∠DFA=∠DFE-∠AFE=45°-28°=17°;
(2)当∠DFC=165°时EF∥BC,理由如下:
∵∠DFC=165°,
∴∠DFA=180°-∠DFC=15°,
∵∠DFE=45°,∴∠AFE=∠DFE-∠DFA=45°-15°=30°,
又∵∠C=30°,∴∠AFE=∠C,
∴EF//BC.


科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
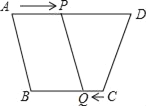
【题目】如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=8cm,P,Q分别从A,C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,_____秒后四边形ABQP是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新新儿童服装店对“天使”牌服装进行调价,其中A型服装每件的价格上调了10%,B型服装每件的价格下调了5%,已知调价前买这两种服装各一件共花费140元,调价后买3件A型服装和2件B型服装共花费350元,则这两种服装在调价前每件各多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图:

(1)根据上图求出下表所缺数据;
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8 | 10 | 1.6 |
(2)根据上表中的平均数、中位数和方差你认为哪班的成绩较好?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空,并在括号内说明理由:
∵BD平分∠ABC(已知)
∴__________=__________(__________)
又∠1=∠D(已知)
∴__________=__________(__________)
∴__________∥__________(__________)
∴∠ABC+__________=180°(__________)
又∠ABC=55°(已知)
∴∠BCD=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交线段BD于E.
(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)画出∠CPQ的角平分线交线段AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
距离地面高度(千米)h | 0 | 1 | 2 | 3 | 4 | 5 |
温度(℃)t | 20 | 14 | 8 | 2 | ﹣4 | ﹣10 |
根据表中,父亲还给小明出了下面几个问题,请你帮助小明回答下列问题:
(1)表中自变量是 ;因变量是 ;当地面上(即h=0时)时,温度是 ℃.
(2)如果用h表示距离地面的高度,用t表示温度,请写出满足t与h关系的式子.
(3)计算出距离地面6千米的高空温度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com