Question

3．把图1的矩形纸片ABCD折叠，B、C两点恰好重合落在AD边上的点P处（如图2）已知∠MPN=90°，PM=3，PN=4．

（1）MN=5；（2）矩形纸片ABCD的面积为28.8．

Answer 1

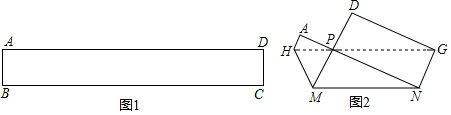
分析 （1）由勾股定理求出MN即可；
（2）根据折叠的性质，得BC的长即为MP+MN+NP=12，再由三角形面积求出PF，得出AB的长，即可求出矩形的面积．

解答 解：（1）∵∠MPN=90°，PM=3，PN=4，
∴MN=$\sqrt{{3}^{2}+{4}^{2}}$=5；
故答案为：5；
（2）BC=MP+MN+NP=12，
作PF⊥MN于F，如图所示：
则AB=PF=$\frac{PM•PN}{MN}$=2.4，
则长方形纸片ABCD的面积=AB•BC=28.8，
故答案为：28.8．

点评 此题主要考查了折叠的性质、勾股定理以及直角三角形的面积公式，利用直角三角形两条直角边的乘积除以斜边得斜边的高是解答此题的关键．