
如下图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
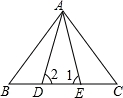
A.AB=AC B.∠BAE=∠CAD C.BE=DC D.AD=DE
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
.如图:某地有两所大学和两条相交叉的公路(点M,N表示大学,AO,BO表示公路).现计划修建一座仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案(要求保留作图痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
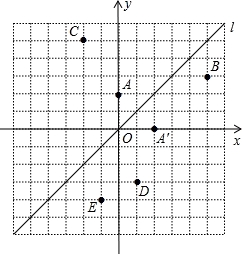
如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
实验与探究:
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′__________、C′__________;
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为__________(不必证明);
运用与拓广:
(3)已知两点D(1,﹣3)、E(﹣1,﹣4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
运动会上,初二(3)班啦啦队,买了两种价格的雪糕,其中甲种雪糕共花费40元,乙种雪糕共花费30元,甲种雪糕比乙种雪糕多20根.乙种雪糕价格是甲种雪糕价格的1.5倍,若设甲种雪糕的价格为x元,根据题意可列方程为( )
A.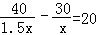 B.
B.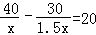
C.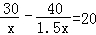 D.
D.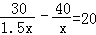
查看答案和解析>>
科目:初中数学 来源: 题型:
问题提出:求边长分别为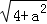 ,
,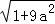 ,
,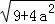 (a为正整数)三角形的面积.
(a为正整数)三角形的面积.
问题探究:为解决上述数学问题,我们采取数形结合和转化的思想方法,并采取一般问题特殊化的策略来进行探究.
探究一:当a=1时,求边长分别为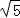 、
、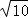 、
、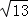 三角形的面积.
三角形的面积.
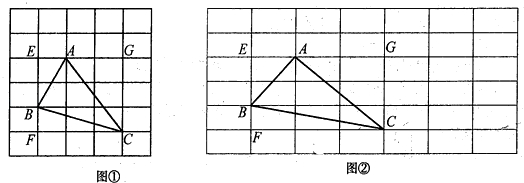
先画一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为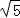 ,
,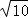 ,
,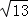 的格点三角形△ABC(如图①).
的格点三角形△ABC(如图①).
因为AB是直角边分别为2和1的Rt△ABE的斜边,所以AB=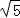 ;
;
因为BC是直角边分别为1和3的Rt△BCF的斜边,所以BC=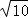 ;
;
因为AC是直角边分别为3和2的Rt△ACG的斜边,所以AC=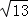 ;通过面积转化,可间接求三角形△ABC的面积.
;通过面积转化,可间接求三角形△ABC的面积.
所以,S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG.
(1)直接写出图①中S△ABC=__________.
探究二:当a=2时,求边长分别为2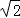 ,
,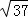 ,5三角形的面积.
,5三角形的面积.
先画一个长方形网格(每个小长方形的长为2,宽为1),再在网格中画出边长分 别为2
别为2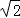 ,
,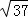 ,5的格点三角形△ABC(如图②).
,5的格点三角形△ABC(如图②).
因为AB是直角边分别为2和2的Rt△ABE的斜边,所以AB=2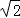 ;
;
因为BC是直角边分别为1和6的Rt△BCF的斜边,所以BC=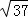 ;
;
因为AC是直角边分别为3和4的Rt△ACG的斜边,所以AC=5,通过面积转化,可间接求三角形△ABC的面积.
所以,S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
(2)直接写出图②中S△ABC=__________.
探究三:当a=3时,求边长分别为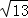 ,
, ,3
,3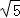 三角形的
三角形的 面积.
面积.

仿照上述方法解答下列问题:
(3)画的长方形网格中,每个小长方形的长应是__________.
(4)边长分别为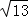 ,
,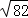 ,3
,3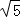 的三角形的面积为__________.
的三角形的面积为__________.
问题解决:求边长分别为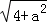 ,
, ,
,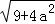 (a为正整数)三角形的面积.
(a为正整数)三角形的面积.
(5)类比上述方法画长方形网格,每个小长方形的长应是__________.
(6)边长分别为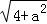 ,
,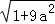 ,
,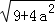 (a为正整数)的三角形的面积是__________.
(a为正整数)的三角形的面积是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com