
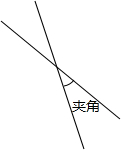
 两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问:
两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问:分析 固定平面上一条直线,其它直线与此条固定直线的交角自这条固定直线起逆时针计算,只能是15°、30°、45°、60°、75°、90°、105°、120°、135°、150°、165°十一种角度之一,所以,平面上最多有12条直线.否则,必有两条直线平行.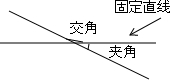
如图,将所有直线做平行移动,使它们交于同一个点,这样的平行移动显然不改变两条直线的“夹角”.无妨设其中一条直线水平,从水平直线开始,逆时针将12条直线分别记为第一条、第二条、…和第十二条直线.然后分以下情况讨论:
(1)第二条至第十二条直线与第一条直线的“夹角”和;
(2)第三条至第十二条直线与第二条直线相交的“夹角”和;
(3)第四条至第十二条直线与第三条直线相交的“夹角”和;
…;
(10)第十一条和第十二条直线与第十条直线相交的“夹角”和;
(11)第十二条直线与第十一条直线相交的“夹角”和.
进一步解决问题.
解答 解:固定平面上一条直线,其它直线与此条固定直线的交角自这条固定直线起逆时针计算,只能是15°、30°、45°、60°、75°、90°、105°、120°、135°、150°、165°十一种角度之一,所以,平面上最多有12条直线.否则,必有两条直线平行.
如图,将所有直线做平行移动,使它们交于同一个点,这样的平行移动显然不改变两条直线的“夹角”.无妨设其中一条直线水平,从水平直线开始,逆时针将12条直线分别记为第一条、第二条、…和第十二条直线.
(1)如图: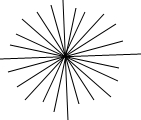
第二条至第十二条直线与第一条直线的“夹角”和是:
15+30+45+60+75+90+75+60+45+30+15=540 (度);
(2)第三条至第十二条直线与第二条直线相交的“夹角”和是:
15+30+45+60+75+90+75+60+45+30=(540-15)(度);
(3)第四条至第十二条直线与第三条直线相交的“夹角”和是:
15+30+45+60+75+90+75+60+45=(540-15-30)(度);
…;
(10)第十一条和第十二条直线与第十条直线相交的“夹角”和是(30+15)(度),
(11)第十二条直线与第十一条直线相交的“夹角”和是:15(度);
将(2)和(11)、(3)和(10)、(4)和(9)、(5)和(8)、(6)和(7)配对,得到所有的“夹角”之和是6×540=3240 (度).
点评 考查了对顶角、邻补角,此题解答的关键在于:固定平面上一条直线,其它直线与此条固定直线的交角自这条固定直线起逆时针计算,分情况讨论,解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BD是菱形ABCD的对角线,点E是边BC上的动点,连接AE,点F在线段AE上,连接BF,DF,且∠AFB=60°,AB=BD
如图,BD是菱形ABCD的对角线,点E是边BC上的动点,连接AE,点F在线段AE上,连接BF,DF,且∠AFB=60°,AB=BD查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com