
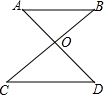
分析 (1)首先根据位似图形的性质可判定△OAB和△ODC相似,再根据相似三角形的性质可判断∠A和∠D的关系,最后根据平行线的判断即可得AB平行于CD;
(2)直接利用相似三角形的判定与性质得出$\frac{AO}{DO}$=$\frac{BO}{CO}$,进而得出答案.
解答 解:(1)AB∥CD;
理由如下:
∵△OAB与△ODC是位似图形,
∴△OAB∽△ODC,
∴∠A=∠D,
∴AB∥CD(内错角相等,两直线平行);
(2)∵△OAB∽△ODC,
∴$\frac{AO}{DO}$=$\frac{BO}{CO}$,
∴$\frac{AO}{3.5}$=$\frac{3}{4}$,
解得:AO=$\frac{21}{8}$.
点评 此题主要考查了位似图形的性质以及相似三角形的判定与性质,正确利用相似三角形性质求出是解题关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
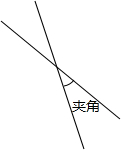 两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问:
两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com