
【题目】已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.求证:(1)BD=AE.(2)若线段AD=5,AB=17,求线段ED的长。
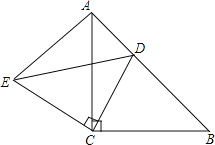
【答案】(1)、证明过程见解析;(2)、13.
【解析】
试题分析:(1)、根据等腰直角三角形的性质得出AC=BC,CD=CE,∠ACD=∠DCE=90°,从而说明∠ACE=∠BCD,然后根据SAS判定三角形全等,从而得到BD=AE;(2)、根据题意得出BD的长度,根据全等从而得到AE的长度以及∠EAD为直角,然后利用Rt△AED的勾股定理求出DE的长度.
试题解析:(1)、∵△ABC和△ECD都是等腰直角三角形, ∴AC=BC,CD=CE, ∵∠ACD=∠DCE=90°,
∴∠ACE+∠ACD=∠BCD+∠ACD, ∴∠ACE=∠BCD,
在△ACE和△BCD中,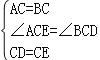 , ∴△ACE≌△BCD(SAS), ∴BD=AE.
, ∴△ACE≌△BCD(SAS), ∴BD=AE.
(2)、∵AD=5, AB=17, ∴BD=17-5=12 ∵△ABC是等腰直角三角形
∴∠B=45°由(1)可知△ACE≌△BCD ∴∠EAC=∠B=45° AE=BD=7
∴∠EAD=90° ∴ED=![]()


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
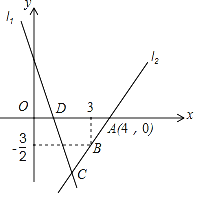
【题目】如图,直线l1的解析表达式为y=﹣3x+3,且l1与x轴交于点D.直线l2经过点A、B,直l1,l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)在直线l2上存在异于点C的另一个点P,使得△ADP与△ADC的面积相等,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm。
(1)若P、Q是△ABC边上的两个动点,其中点P从A沿A→B方向运动,速度为每秒1cm,点Q从B沿B→C方向运动,速度为每秒2cm,两点同时出发,设出发时间为t秒.①当t=1秒时,求PQ的长;②从出发几秒钟后,△PQB是等腰三角形?
(2)若M在△ABC边上沿B→A→C方向以每秒3cm的速度运动,则当点M在边CA上运动时,求△BCM成为等腰三角形时M运动的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com