练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，为了测量大树的高度，小华在B处垂直竖立起一根长为2.5m的木杆，当他站在点F处时，他的眼睛E、木杆的顶端A、树端C恰好在同一条直线上，量得BF=3m，BD=9m，小华的眼睛E与地面的距离EF为1.5m，求大树的高度．
    分析：先过E作EN⊥AB，交AB于N点交CD于M点，可以构造矩形，利用平行线分线段成比例定理的推论易得△ECM∽△EAN，再利用比例线段，可求CM，进而可求CD．
    解答：解：如图，过E作EN⊥AB，交AB于N点交CD于M点，
    由题意知，MN=BD=9m，EM=FD=12m，NB=MD=EF=1.5m，则AN=2.5-1.5=1m，
    ∵CM∥AN，
    ∴△ECM∽△EAN，
    ∴CM：AN=EM：EN，
    ∴CM=1.2m，
    ∴CD=CM+DM=1.2+1.5=2.7m，
    所以树高为2.7m．
    点评：本题考查了相似三角形的判定和性质，解题的关键是利用平行线分线段成比例定理的推论得出△ECM∽△EAN．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

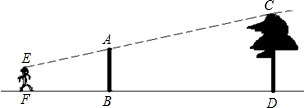
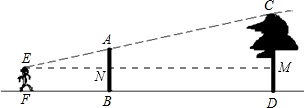
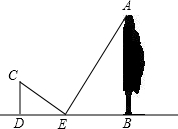    精英家教网如图，为了测量校园内一棵大树的高度，小丽同学把一面小圆镜放在与树相距20米处的E点，然后后退2米至D点，恰好可以从镜中观察到树顶A点，若该同学身高1.6米，你能求出树的高度吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，为了测量河宽，在河的一边沿岸选取A、B两点，对岸岸边有一块石头C．在△ABC中，测得∠A=60°，∠B=45°，AB=60米．
    （1）求河宽（用精确值表示，保留根号）；
    （2）如果对岸岸边有一棵大树D，且CD∥AB，并测得∠DAB=37°，求C、D两点之间的距离（结果精确到0.1米）．（参考数据：
    		2
    ≈1.41    ，
    		3
    ≈1.73    ，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，cot37°≈1.33）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，为了测量大树的高度，小华在B处垂直竖立起一根长为2.5m的木杆，当他站在点F处时，他的眼睛E、木杆的顶端A、树端C恰好在同一条直线上，量得BF=3m，BD=9m，小华的眼睛E与地面的距离EF为1.5m，求大树的高度．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年江苏省南通市海门市九年级（上）期末数学试卷（解析版） 题型：解答题

    如图，为了测量大树的高度，小华在B处垂直竖立起一根长为2.5m的木杆，当他站在点F处时，他的眼睛E、木杆的顶端A、树端C恰好在同一条直线上，量得BF=3m，BD=9m，小华的眼睛E与地面的距离EF为1.5m，求大树的高度．

    查看答案和解析>>

    同步练习册答案