
分析 (1)根据对称轴公式求出b,再将P代入抛物线得到c,求出抛物线解析式,根据Q点的横坐标即可解决问题.
(2)由题意可以假设直线PQ为y=-2x+b′,利用方程组求出点Q坐标,分两种情形①-1≤b≤0时,②-4<b∠-1时,构建二次函数,根据二次函数的性质即可解决问题.
解答 解:(1)由题意:-$\frac{b}{2a}$=2,a=1,
∴b=-4,∴抛物线为y=x2-4x+c,将P(2,-c)代入得到,-c=4-8+c,
∴c=2,
∴抛物线解析式为y=x2-4x+2,
∵点Q横坐标为-1,
∴x=-1时,y=7
∴点Q坐标为(-1,7).
(2)由题意可以假设直线PQ为y=-2x+b′,
∵顶点P(-$\frac{b}{2}$,-1),代入上式得到:-1=b+b′,
∴b′=-1-b,
∴直线PQ为y=-2x-1-b,∴点M坐标(0,-1-b),
由 $\left\{\begin{array}{l}{y=-2x-1-b}\\{y={x}^{2}+bx+\frac{{b}^{2}-4}{4}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{b}{2}}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2-\frac{b}{2}}\\{y=3}\end{array}\right.$
∴点Q坐标(-2-$\frac{b}{2}$,3),
∵-4<b≤0,
①-1≤b≤0时,
∴S△OQM=$\frac{1}{2}$•(2+$\frac{b}{2}$)•(1+b)=$\frac{1}{4}$(b+$\frac{5}{2}$)2-$\frac{9}{16}$,
∴b=0时,△OQM的面积最大,最大值为1.
②-4<b∠-1时,
S△OQM=$\frac{1}{2}$•(2+$\frac{b}{2}$)•(-1-b)=-$\frac{1}{4}$(b+$\frac{5}{2}$)2+$\frac{9}{16}$,
∵-$\frac{1}{4}$<0,
∴b=-$\frac{5}{2}$时,△OQM的面积最大,最大值为$\frac{9}{16}$,
综上所述,△OQM的面积的最大值为1.
点评 本题考查二次函数的性质、待定系数法,解题的关键是灵活运用待定系数法解决问题,学会利用方程组求交点坐标,题目比较难,学会分类讨论的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
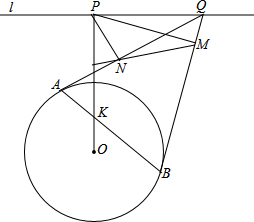 如图,圆O(圆心为O)与直线l相离,作OP⊥l,P为垂足.设点Q是l上任意一点(不与点P重合),过点Q作圆O的两条切线QA和QB,A和B为切点,AB与OP相交于点K.过点P作PM⊥QB,PN⊥QA,M和N为垂足.求证:直线MN平分线段KP.
如图,圆O(圆心为O)与直线l相离,作OP⊥l,P为垂足.设点Q是l上任意一点(不与点P重合),过点Q作圆O的两条切线QA和QB,A和B为切点,AB与OP相交于点K.过点P作PM⊥QB,PN⊥QA,M和N为垂足.求证:直线MN平分线段KP.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
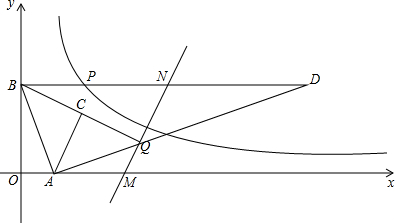
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com