
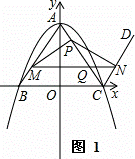
如图1,在平面直角坐标系中,二次函数y=﹣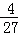 x2+12的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连接AB,AC.
x2+12的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连接AB,AC.
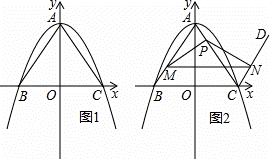
(1)点B的坐标为 ,点C的坐标为 ;
(2)过点C作射线CD∥AB,点M是线段AB上的动点,点P是线段AC上的动点,且始终满足BM=AP(点M不与点A,点B重合),过点M作MN∥BC分别交AC于点Q,交射线CD于点N (点 Q不与点P重合),连接PM,PN,设线段AP的长为n.
①如图2,当n< AC时,求证:△PAM≌△NCP;
AC时,求证:△PAM≌△NCP;
②直接用含n的代数式表示线段PQ的长;
③若PM的长为 ,当二次函数y=﹣
,当二次函数y=﹣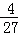 x2+12的图象经过平移同时过点P和点N时,请直接写出此时的二次函数表达式.
x2+12的图象经过平移同时过点P和点N时,请直接写出此时的二次函数表达式.
解:(1)答:(﹣9,0),(9,0).
B、C为抛物线与x轴的交点,故代入y=0,得y=﹣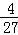 x2+12=0,
x2+12=0,
解得 x=﹣9或x=9,
即B(﹣9,0),C(9,0).
(2)①证明:∵AB∥CN,
∴∠MAP=∠PCN,
∵MN∥BC,
∴四边形MBCN为平行四边形,
∴BM=CN,
∵AP=BM,
∴AP=CN,
∵BO=OC,OA⊥BC,
∴OA垂直平分BC,
∴AB=AC,
∴AM=AB﹣BM=AC﹣AP=CP.
在△MAP和△PCN中,
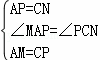 ,
,
∴△MAP≌△PCN(AAS).
②解:1.当n<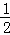 AC时,如图1,
AC时,如图1,
 ,
,
∵四边形MBCN为平行四边形,
∴∠MBC=∠QNC,
∵AB=AC,MN∥BC,
∴∠MBC=∠QCB=∠NQC,
∴∠NQC=∠QNC,
∴CN=CQ,
∵△MAP≌△PCN,
∴AP=CN=CQ,
∵AP=n,AC=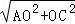 =
=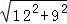 =15,
=15,
∴PQ=AC﹣AP﹣QC=15﹣2n.
2.当n=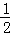 AC时,显然P、Q重合,PQ=0.
AC时,显然P、Q重合,PQ=0.
3.当n>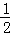 AC时,如图2,
AC时,如图2,
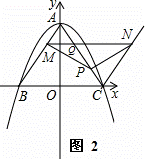
∵四边形MBCN为平行四边形,
∴∠MBC=∠QNC,BM=CN
∵AB=AC,MN∥BC,
∴∠MBC=∠QCB=∠NQC,
∴∠NQC=∠QNC,
∴BM=CN=CQ,
∵AP=BM,
∴AP=CQ,
∵AP=n,AC=15,
∴PQ=AP+QC﹣AC=2n﹣15.
综上所述,当n≤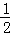 AC时,PQ=15﹣2n;当n>
AC时,PQ=15﹣2n;当n>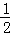 AC时,PQ=2n﹣15.
AC时,PQ=2n﹣15.
③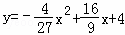 或
或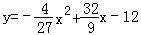 .
.
分析如下:
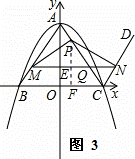
1.当n≤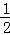 AC时,如图3,过点P作x轴的垂线,交MN于E,交BC于F.
AC时,如图3,过点P作x轴的垂线,交MN于E,交BC于F.
此时△PEQ∽△PFC∽△AOC,PQ=15﹣2n.
∵PM=PN,
∴ME=EN=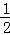 MN=
MN=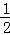 BC=9,
BC=9,
∴PE=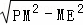 =
=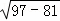 =4,
=4,
∵OC:OA:AC=3:4:5,△PEQ∽△PFC∽△AOC,
∴PQ=5,
∴15﹣2n=5,
∴AP=n=5,
∴PC=10,
∴FC=6,PF=8,
∵OF=OC﹣FC=9﹣6=3,EN=9,EF=PF﹣PE=8﹣4=4,
∴P(3,8),N(12,4).
设二次函数y=﹣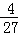 x2+12平移后的解析式为y=﹣
x2+12平移后的解析式为y=﹣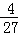 (x+k)2+12+h,
(x+k)2+12+h,
∴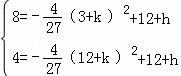 ,
,
解得 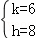 ,
,
∴y=﹣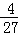 (x+6)2+12+8=﹣
(x+6)2+12+8=﹣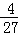 x2+
x2+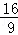 x+4.
x+4.
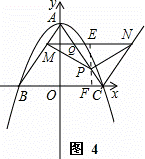
2.当n>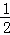 AC时,如图4,过点P作x轴的垂线,交MN于E,交BC于F.
AC时,如图4,过点P作x轴的垂线,交MN于E,交BC于F.
此时△PEQ∽△PFC∽△AOC,PQ=2n﹣15.
∵PM=PN,
∴ME=EN=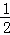 MN=
MN=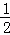 BC=9,
BC=9,
∴PE=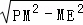 =
=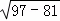 =4,
=4,
∵OC:OA:AC=3:4:5,△PEQ∽△PFC∽△AOC,
∴PQ=5,
∴2n﹣15=5,
∴AP=n=10,
∴PC=5,
∴FC=3,PF=4,
∵OF=OC﹣FC=9﹣3=6,EN=9,EF=PF+PE=4+4=8,
∴P(6,4),N(15,8).
设二次函数y=﹣ x2+12平移后的解析式为y=﹣
x2+12平移后的解析式为y=﹣ (x+k)2+12+h,
(x+k)2+12+h,
∴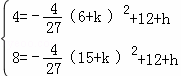 ,
,
解得 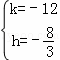 ,
,
∴y=﹣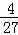 (x﹣12)2+12﹣
(x﹣12)2+12﹣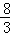 =﹣
=﹣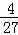 x2+
x2+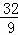 x﹣12.
x﹣12.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是( )
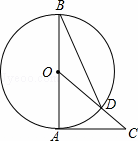
A. 30° B. 25° C. 20° D. 15°
查看答案和解析>>
科目:初中数学 来源: 题型:
四川省“单独两孩”政策于2014年3月20日正式开始实施,该政策的实施可能给我们的生活带来一些变化,绵阳市人口计生部门抽样调查了部分市民(每个参与调查的市民必须且只能在以下6种变化中选择一项),并将调查结果绘制成统计图:
种类 A B C D E F
变化 有利于延缓社会老龄化现象 导致人口暴增 提升家庭抗风险能力 增大社会基本公共服务的压力 环节男女比例不平衡现象 促进人口与社会、资源、环境的协调可持续发展
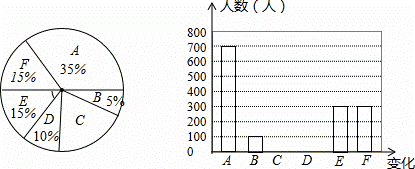
根据统计图,回答下列问题:
(1)参与调查的市民一共有 人;
(2)参与调查的市民中选择C的人数是 人;
(3)∠α= ;
(4)请补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
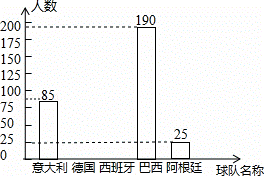
2014年世界杯足球赛于北京时间6月 13日 2时在巴西开 幕,某媒体足球栏目从参加世界杯球队中选出五支传统强队:意 大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最 有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被 调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一 队作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:
| 球队名称 | 百分比 |
| 意大利 | 17% |
| 德国 | a |
| 西班牙 | 10% |
| 巴西 | 38% |
| 阿根廷 | 0 |
根据统计图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)根据以上信息,请直接在答题卡中补全条形统计图;
(3)根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.
查看答案和解析>>
科目:初中数学 来源: 题型:
某篮球队12名队员的年龄如表:
| 年龄(岁) | 18 | 19 | 20 | 21 |
| 人数 | 5 | 4 | 1 | 2 |
则这12名队员年龄的众数和平均数分别是( )
|
| A. | 18,19 | B. | 19,19 | C. | 18,19.5 | D. | 19,19.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系xOy中,对于点P(x,y),我们把点P(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(3,1),则点A3的坐标为 ,点A2014的坐标为 ;若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
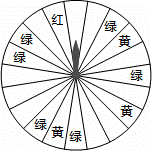
某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com