
【题目】如图所示,CD是⊙O的弦,AB是⊙O的直径,且CD//AB,连接AC,AD,OD,其中AC=CD,过点B的切线交CD的延长线于E. 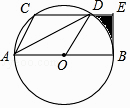
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分图形的周长(结果精确到1,参考数据:π=3.1, ![]() =1.4,
=1.4, ![]() =1.7).
=1.7).
【答案】
(1)证明:∵CD//AB,
∴∠CDA=∠DAO,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠CDA=∠ADO,
∴DA平分∠CDO
(2)解:∵AC=CD,
∴∠CDA=∠CAD,
∵∠CDA=∠ADO,
∴∠CAD=∠ADO,
∴AC//OD,
又∵AC=CD,CD//AB,
∴四边形AODC是菱形,
∴OA=AC,
连接OC,∵AB=12,
∴OA=AC=OC=6,
∴∠CAO=60°,
作CF⊥AB于点F,
∴CF=ACsin60°=6× ![]() =3
=3 ![]() ,AF=ACcos60°=3,
,AF=ACcos60°=3,
∵EB⊥AB,CD//AB,
则BE=CF=3 ![]() ,DE=AB﹣AF﹣CD=12﹣3﹣6=3,
,DE=AB﹣AF﹣CD=12﹣3﹣6=3,
∵∠CAO=60°,AC//DO,
∴∠CAO=∠DOB=60°,
∴ ![]() ,
,
∴图中阴影部分图形的周长是: ![]() =2π+3
=2π+3 ![]() +3=2×3.1+3×1.7+3≈14.
+3=2×3.1+3×1.7+3≈14.
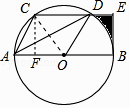
【解析】(1)要求DA平分∠CDO,只要求得∠CDA=∠ADO成立即可,根据题目中的条件,可以得到∠CDA=∠ADO,从而可以解答本题;(2)图中阴影部分图形的周长是BE+DE+ ![]() 的长,根据(1)中的结论和题目中的条件,可以求得BE+DE+
的长,根据(1)中的结论和题目中的条件,可以求得BE+DE+ ![]() 的长,从而可以解答本题.
的长,从而可以解答本题.
【考点精析】通过灵活运用切线的性质定理和弧长计算公式,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1 , B2 , B3 , …,则B2017的坐标为( )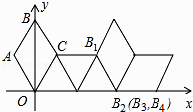
A.(1345,0)
B.(1345.5, ![]() )
)
C.(1345, ![]() )
)
D.(1345.5,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:
不成立,但有些数可以使得它成立,例如: ![]() .我们称使得
.我们称使得![]() 成立的一对数
成立的一对数![]() ,
, ![]() 为“相伴数对”,记为
为“相伴数对”,记为![]() .
.
(1)若![]() 是“相伴数对”,求
是“相伴数对”,求![]() 的值;
的值;
(2)写出一个“相伴数对” ![]() ,其中
,其中![]() 且
且![]() ;
;
(3)若![]() 是“相伴数对”,求代数式
是“相伴数对”,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
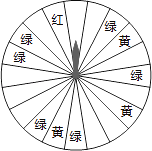
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行摸排游戏,现有三张形状大小完全相同的牌,正面分别标有数字2,3,5,将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法写出所有可能的结果;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
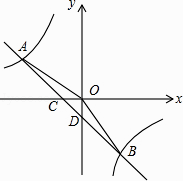
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC= ![]() .
. 
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国主要银行的商标设计基本上都融入了中国古代钱币的图案,下图中我国四大银行的商标图案中既是轴对称图形又是中心对称图形的个数有( ) 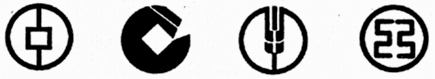
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图![]() ,点
,点![]() 是线段
是线段![]() 上一定点,
上一定点,![]() ,
,![]() 、
、![]() 两点分别从
两点分别从![]() 、
、![]() 出发以
出发以![]() 、
、![]() 的速度沿直线
的速度沿直线![]() 向左运动,运动方向如箭头所示(
向左运动,运动方向如箭头所示(![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 上)
上)
![]() 若
若![]() ,当点
,当点![]() 、
、![]() 运动了
运动了![]() ,此时
,此时![]() ________,
________,![]() ________;(直接填空)
________;(直接填空)
![]() 当点
当点![]() 、
、![]() 运动了
运动了![]() ,求
,求![]() 的值.
的值.
![]() 若点
若点![]() 、
、![]() 运动时,总有
运动时,总有![]() ,则
,则![]() ________(填空)
________(填空)
![]() 在
在![]() 的条件下,
的条件下,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值.
的值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com