
【题目】二次函数图象的顶点在原点O,经过点A(1, ![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.

(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,且在y轴的右侧。过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
【答案】(1)y=![]() x2(2)证明见解析(3) (
x2(2)证明见解析(3) (![]() ,3)或(﹣
,3)或(﹣![]() ,3)
,3)
【解析】试题分析:(1)根据题意可设函数的解析式为y=ax2,将点A代入函数解析式,求出a的值,继而可求得二次函数的解析式;
(2)过点P作PB⊥y轴于点B,利用勾股定理求出PF,表示出PM,可得PF=PM,∠PFM=∠PMF,结合平行线的性质,可得出结论;
(3)首先可得∠FMH=30°,设点P的坐标为(x, ![]() x2),根据PF=PM=FM,可得关于x的方程,求出x的值即可得出答案.
x2),根据PF=PM=FM,可得关于x的方程,求出x的值即可得出答案.
试题解析:(1)∵二次函数图象的顶点在原点O,
∴设二次函数的解析式为y=ax2,
将点A(1, ![]() )代入y=ax2得:a=
)代入y=ax2得:a=![]() ,
,
∴二次函数的解析式为y=![]() x2;
x2;
(2)∵点P在抛物线y=![]() x2上,
x2上,
∴可设点P的坐标为(x, ![]() x2),
x2),
过点P作PB⊥y轴于点B,则BF=|![]() x2﹣1|,PB=|x|,
x2﹣1|,PB=|x|,
∴Rt△BPF中,
PF= =
=![]() x2+1,
x2+1,
∵PM⊥直线y=﹣1,
∴PM=![]() x2+1,
x2+1,
∴PF=PM,
∴∠PFM=∠PMF,
又∵PM∥y轴,
∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP;
(3)当△FPM是等边三角形时,∠PMF=60°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,
∴![]() x2+1=4,
x2+1=4,
解得:x=±2![]() ,
,
∴![]() x2=
x2=![]() ×12=3,
×12=3,
∴满足条件的点P的坐标为(2![]() ,3)或(﹣2
,3)或(﹣2![]() ,3).
,3).



 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
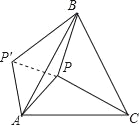
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由6个大小相同的小正方形组成的方格中,设每个小正方形的边长均为1.
(1)如图①,![]() ,
,![]() ,
,![]() 是三个格点(即小正方形的顶点),判断
是三个格点(即小正方形的顶点),判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;

(2)如图②,连接三格和两格的对角线,求![]() 的度数(要求:画出示意图,并写出证明过程).
的度数(要求:画出示意图,并写出证明过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
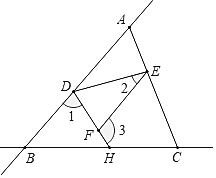
【题目】如图,直线AB和直线BC相交于点B,连接AC,点D、E、H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°.
(1)求证:∠CEF=∠EAD;
(2)若DH平分∠BDE,∠2=![]() 求∠3的度数(用含
求∠3的度数(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于点O,AC=2,BD=2![]() ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.

(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:①当
的四个命题:①当![]() 时,
时, ![]() 有最小值10;②
有最小值10;②![]() 为任意实数,
为任意实数, ![]() 时的函数值大于
时的函数值大于![]() 时的函数值;③若
时的函数值;③若![]() ,且
,且![]() 是整数,当
是整数,当![]() 时,
时, ![]() 的整数值有
的整数值有![]() 个;④若函数图象过点
个;④若函数图象过点![]() 和
和![]() ,其中
,其中![]() ,
, ![]() ,则
,则![]() .其中真命题的序号是( )
.其中真命题的序号是( )
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1已知:∠B=25°,∠BED=80°,∠D=55°.探究AB与CD有怎样的位置关系.
(2)如图2已知AB∥EF,试猜想∠B,∠F,∠BCF之间的关系,写出这种关系,并加以证明.
(3)如图3已知AB∥CD,试猜想∠1,∠2,∠3,∠4,∠5之间的关系,请直接写出这种关系,不用证明.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com