
【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.

(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/分钟 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
频数(通话次数) | 20 | 16 | 9 | 5 |
则5月份通话次数中,通话时间不超过15分钟的所占百分比是( )
A. 10% B. 40% C. 50% D. 90%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,一次函数y=kx+b的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
, ![]() 两点.
两点.
(1)求一次函数和反比例函数的解析式;
(2)设点![]() 和
和![]() 是反比例函数
是反比例函数![]() 图象上两点,若
图象上两点,若![]() ,求
,求![]() 的值;
的值;
(3)若M(x1,y1)和N(x2,y2)两点在直线AB上,如图2所示,过M、N两点分别作y轴的平行线交双曲线于E、F,已知﹣3<x1<0,x2>1,请探究当x1、x2满足什么关系时,MN∥EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB高16米,远处有一塔CD,某人在楼底B处测得塔顶的仰角为38.5°,爬到楼顶A处测得塔顶的仰角为22°,求塔高CD及大楼与塔之间的距离BD的长.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80 )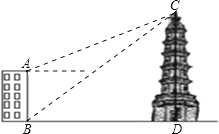
查看答案和解析>>
科目:初中数学 来源: 题型:
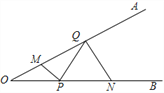
【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长均为1的7×7网格图中,格点上有A,B,C,D,E五个定点,如图所示,一个动点P从点E出发,绕点A逆时针旋转90°,之后该动点继续绕点B,C,D逆时针90°后回到初始位置,点P运转路线的总长是 . (结果保留π)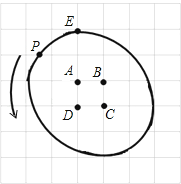
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC,求证:∠A+∠B+∠C=180°.
通过画平行线,将∠A、∠B、∠C作等角代换,使各角之和恰为一平角,依辅助线不同而得多种证法.

证法1:如图1,延长BC到D,过C画CE∥BA.
∵BA∥CE(作图2所知),
∴∠B=∠1,∠A=∠2(两直线平行,同位角、内错角相等).
又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换).
如图3,过BC上任一点F,画FH∥AC,FG∥AB,这种添加辅助线的方法能证明∠A+∠B+∠C=180°吗?请你试一试.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 是一个长为
是一个长为![]() 、宽为
、宽为![]() 的长方形(其中
的长方形(其中![]() ,
,![]() 均为正数,且
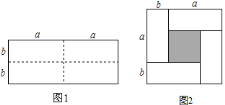
均为正数,且![]() ),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图
),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图![]() 方式拼成一个大正方形.
方式拼成一个大正方形.
如图![]() 是一个长为
是一个长为![]() 、宽为
、宽为![]() 的长方形(其中
的长方形(其中![]() ,
,![]() 均为正数,且
均为正数,且![]() ),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图
),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图![]() 方式拼成一个大正方形.
方式拼成一个大正方形.
![]() 你认为图
你认为图![]() 中大正方形的边长为________;小正方形(阴影部分)的边长为________.(用含
中大正方形的边长为________;小正方形(阴影部分)的边长为________.(用含![]() 、
、![]() 的代数式表示)
的代数式表示)
![]() 仔细观察图
仔细观察图![]() ,请你写出下列三个代数式:
,请你写出下列三个代数式:![]() ,
,![]() ,
,![]() 所表示的图形面积之间的相等关系,并选取适合
所表示的图形面积之间的相等关系,并选取适合![]() 、
、![]() 的数值加以验证.
的数值加以验证.
![]() 已知
已知![]() ,
,![]() .求代数式
.求代数式![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com