
【题目】如图1,已知△ABC,求证:∠A+∠B+∠C=180°.
通过画平行线,将∠A、∠B、∠C作等角代换,使各角之和恰为一平角,依辅助线不同而得多种证法.

证法1:如图1,延长BC到D,过C画CE∥BA.
∵BA∥CE(作图2所知),
∴∠B=∠1,∠A=∠2(两直线平行,同位角、内错角相等).
又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换).
如图3,过BC上任一点F,画FH∥AC,FG∥AB,这种添加辅助线的方法能证明∠A+∠B+∠C=180°吗?请你试一试.
科目:初中数学 来源: 题型:
【题目】勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉.生活中到处可见黄金分割的美.如图,线段AB=1,点P1是线段AB的黄金分割点(AP1<BP1),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则APn的长度是 . ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.

(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级从甲乙两位同学中选派一人参加“秀美山河”知识竞赛,老师对他们的五次模拟成绩(单位:分)进行了整理,美工计算出甲成绩的平均数是80,甲乙成绩的方差分别是320,40,但绘制的统计图尚不完整.
甲乙两人模拟成绩统计表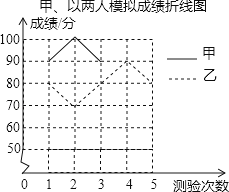
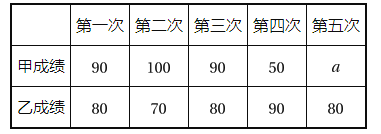
根据以上信息,请你解答下列问题:
(1)a=;
(2)请完成图中表示甲成绩变化情况的折线;
(3)求乙成绩的平均数;
(4)从平均数和方差的角度分析,谁将被选中.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,且
,且![]() 、
、![]() 满足
满足![]()
![]()
![]() 点
点![]() 表示的数为________;点
表示的数为________;点![]() 表示的数为________.
表示的数为________.
![]() 若点
若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 点表示的数________.
点表示的数________.
![]() 若在原点
若在原点![]() 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点![]() 处以
处以![]() 个单位/秒的速度向左运动;同时另一小球乙从点
个单位/秒的速度向左运动;同时另一小球乙从点![]() 处以
处以![]() 个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为
个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为![]() (秒),请分别表示出甲、乙两小球到原点的距离(用含
(秒),请分别表示出甲、乙两小球到原点的距离(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小梅将边长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …长的若干个正方形按一定规律拼成不同的长方形,如图所示.
…长的若干个正方形按一定规律拼成不同的长方形,如图所示.
![]() 求第四个长方形的周长;
求第四个长方形的周长;
![]() 当
当![]() 时,求第五个长方形的面积.(用科学记数法表示)
时,求第五个长方形的面积.(用科学记数法表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com