练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正三角形和正方形的面积分别为10，6，两阴影部分的面积分别为a，b（a＞b），则（a﹣b）等于 ．

    【答案】4
    【解析】解：设重叠部分的面积为x，
    则正三角形的面积为：a+x=10①，
    正方形的面积为：b+x=6②，
    ①﹣②得，a﹣b=4．
    所以答案是：4．
    【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识，掌握等边三角形的三个角都相等并且每个角都是60°，以及对正方形的性质的理解，了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校计划购买篮球、排球共20个，购买2个篮球，3个排球，共需花费190元；购买3个篮球的费用与购买5个排球的费用相同。

    (1)篮球和排球的单价各是多少元?

    (2)若购买篮球不少于8个，所需费用总额不超过800元.请你求出满足要求的所有购买方案，并直接写出其中最省钱的购买方案

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某企业生产部统计了15名工人某月的加工零件数：

    每人加工零件数

    540

    450

    300

    240

    210

    120

    人数

    1

    1

    2

    6

    3

    2

    （1）求出这15人该月加工零件数的平均数并直接写出中位数和众数；

    （2）若生产部领导把每位工人的月加工零件数定为260件，你认为合理否，为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠AOB＝30°，点M、N分别在边OA、OB上，且OM＝1，ON＝3，点P、Q分别在边OB、OA上，则MP＋PQ＋QN的最小值是____________

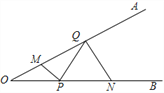
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，方格纸每个小方格是边长为1个单位长度的正方形，在平面直角坐标系中，点A（1，0），B（5，0），C（a，b）D（1，4）．

    （1）描出A、B、C、D四点的位置．如图，则a=　　；b=　　；

    （2）四边形ABCD的面积是　　；（直接写出结果）

    （3）把四边形ABCD向左平移6个单位，再向下平移1个单位得到四边形A'B'C'D'，在图中画出四边形A'B'C'D'，并写出A'B'C'D'的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知△ABC，求证：∠A+∠B+∠C=180°．

    通过画平行线，将∠A、∠B、∠C作等角代换，使各角之和恰为一平角，依辅助线不同而得多种证法．

    证法1：如图1，延长BC到D，过C画CE∥BA．

    ∵BA∥CE（作图2所知），

    ∴∠B=∠1，∠A=∠2（两直线平行，同位角、内错角相等）．

    又∵∠BCD=∠BCA+∠2+∠1=180°（平角的定义），

    ∴∠A+∠B+∠ACB=180°（等量代换）．

    如图3，过BC上任一点F，画FH∥AC，FG∥AB，这种添加辅助线的方法能证明∠A+∠B+∠C=180°吗？请你试一试．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某单位计划用3天时间进行设备检修，安排小王，小李，小赵三位工程师各带班一天，带班顺序是随机确定的．
    （1）请你写出三天带班顺序的所有可能的结果；
    （2）求小李和小赵恰好相邻的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边△ABC中，点D是 AB边上一点，连接CD，将线段CD绕点C按顺时针方向旋转60°后得到CE，连接AE．求证：AE∥BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在数学中，有许多关系都是在不经意间被发现的．当然，没有敏锐的观察力是做不到的．数学家们往往是这样来研究问题的：特值探究–猜想归纳–逻辑证明–总结应用．下面我们也来像数学家们那样分四步找出这两个代数式的关系：对于代数式与．

    特值探究：

    当，时，________；________

    当，时，________；________

    猜想归纳：

    观察的结果，写出与的关系：________．

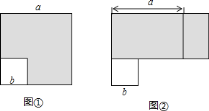
    逻辑证明：如图，边长为的正方形纸片剪出一个边长为的小正方形之后，剩余部分（即阴影部分）又剪拼成一个矩形（不重叠无缝隙），请你说说是如何用这个图来得出中的关系？

    总结应用：利用你发现的关系，求：

    ①若，且，则________；

    ②的值．（提示：你可能要用到公式）

    查看答案和解析>>

    同步练习册答案