【题目】小梅将边长分别为
，
，
，
，
，
…长的若干个正方形按一定规律拼成不同的长方形，如图所示．
求第四个长方形的周长；
当
时，求第五个长方形的面积．（用科学记数法表示）
【答案】(1)26m;(2)
【解析】
（1）根据第一个的周长为：2（1+2）m，第二个的周长为：2（2+3）m，第三个的周长为：2（3+5）m，可得第四个的周长为：2（5+8）m，据此可得第四个长方形的周长；
（2）根据（1）中的规律可得：第五个长方形的宽为8m，长为13m，据此可得当m=100时，第五个长方形的面积为800×1300=1.04×106．
（1）第一个的周长为：2（1+2）m，第二个的周长为：2（2+3）m，第三个的周长为：2（3+5）m，第四个的周长为：2（5+8）m，即第四个长方形的周长为26m；
（2）由此可推出第n个长方形的宽为第n﹣1个长方形的长，第n个长方形的长为第n﹣1个长方形的长和宽的和．
可得：第五个长方形的宽为8m，长为13m，∴当m=100时，第五个长方形的面积为800×1300=1.04×106．
科目：初中数学 来源： 题型：
【题目】如图1，已知△ABC，求证：∠A+∠B+∠C=180°．
通过画平行线，将∠A、∠B、∠C作等角代换，使各角之和恰为一平角，依辅助线不同而得多种证法．
证法1：如图1，延长BC到D，过C画CE∥BA．
∵BA∥CE（作图2所知），
∴∠B=∠1，∠A=∠2（两直线平行，同位角、内错角相等）．
又∵∠BCD=∠BCA+∠2+∠1=180°（平角的定义），
∴∠A+∠B+∠ACB=180°（等量代换）．
如图3，过BC上任一点F，画FH∥AC，FG∥AB，这种添加辅助线的方法能证明∠A+∠B+∠C=180°吗？请你试一试．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了丰富少年儿童的业余生活，某社区要在如图中的AB所在的直线上建一图书室，本社区有两所学校所在的位置在点C和点D处，CA⊥AB于A，DB⊥AB于B.已知AB=2.5km，CA=1.5km，DB=1.Okm，试问：图书室E应该建在距点A多少km处，才能使它到两所学校的距离相等？
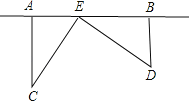
查看答案和解析>>
科目：初中数学 来源： 题型：
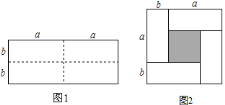
【题目】如图
是一个长为
、宽为
的长方形（其中
，
均为正数，且
），沿图中虚线用剪刀均匀分成四块相同小长方形，然后按图
方式拼成一个大正方形．
如图是一个长为、宽为的长方形（其中，均为正数，且），沿图中虚线用剪刀均匀分成四块相同小长方形，然后按图方式拼成一个大正方形．
你认为图中大正方形的边长为________；小正方形（阴影部分）的边长为________．（用含、的代数式表示）
仔细观察图，请你写出下列三个代数式：
，
，
所表示的图形面积之间的相等关系，并选取适合、的数值加以验证．
已知
，
．求代数式
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在数学中，有许多关系都是在不经意间被发现的．当然，没有敏锐的观察力是做不到的．数学家们往往是这样来研究问题的：特值探究–猜想归纳–逻辑证明–总结应用．下面我们也来像数学家们那样分四步找出这两个代数式的关系：对于代数式
与
．
特值探究：
当
，
时，
________；
________
当
，
时，________；________
猜想归纳：
观察的结果，写出与的关系：________．
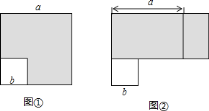
逻辑证明：如图，边长为
的正方形纸片剪出一个边长为
的小正方形之后，剩余部分（即阴影部分）又剪拼成一个矩形（不重叠无缝隙），请你说说是如何用这个图来得出中的关系？
总结应用：利用你发现的关系，求：
①若
，且
，则
________；
②
的值．（提示：你可能要用到公式
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某一工程，在工程招标时，接到甲、乙两个工程队的投标书．施工一天，需付甲工程队工程款1.2万元，乙工程队工程款0.5万元．工程领导小组根据甲、乙两队的投标书测算，有如下方案：
（1）甲队单独完成这项工程刚好如期完成；
（2）乙队单独完成这项工程要比规定日期多用6天；
（3）若甲、乙两队合作3天，余下的工程由乙队单独做也正好如期完成．
试问：(1)规定日期是多少天？
(2)在不耽误工期的前提下，你觉得哪一种施工方案最节省工程款？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线的对称轴是直线x=2，顶点A的纵坐标为1，点B（4，0）在此抛物线上．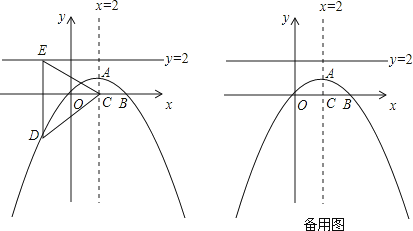
（1）求此抛物线的解析式；
（2）若此抛物线对称轴与x轴交点为C，点D（x，y）为抛物线上一动点，过点D作直线y=2的垂线，垂足为E．
①用含y的代数式表示CD2 ， 并猜想CD2与DE2之间的数量关系，请给出证明；
②在此抛物线上是否存在点D，使∠EDC=120°？如果存在，请直接写出D点坐标；如果不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
（1）
（2）
（3）(－2
)－(＋4.7)－(－0.4)＋ (－3.3) （4）
（5）
（6）（
-
+
）×（-36）
（7）
（8）—
(用简便方法计算)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠C=90°，AC=8cm，BC=6cm，点P、Q同时从点C出发，以1cm/s的速度分别沿CA、CB匀速运动．当点Q到达点B时，点P、Q同时停止运动．过点P作AC的垂线l交AB于点R，连接PQ、RQ，并作△PQR关于直线l对称的图形，得到△PQ′R．设点Q的运动时间为t（s），△PQ′R与△PAR重叠部分的面积为S（cm2）．
（1）t为何值时，点Q′恰好落在AB上？
（2）求S与t的函数关系式，并写出t的取值范围；
（3）S能否为 
cm2？若能，求出此时的t值；若不能，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com