
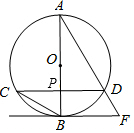
 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.分析 (1)欲证明直线BF是⊙O的切线,只要证明AB⊥BF即可.
(2)连接OC,设OC=OB=x,则PB=x-1,解直角三角形求得PC=2(x-1),在Rt△OPC中,利用勾股定理求出OB=$\frac{5}{3}$,进而求得PD=PC=$\frac{4}{3}$,AB=$\frac{10}{3}$,AP=$\frac{8}{3}$由△APD∽△ABF,$\frac{AP}{AB}$=$\frac{PD}{BF}$,即可解决问题.
解答 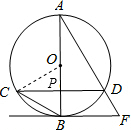 (1)证明:∵∠AFB=∠ABC,∠ABC=∠ADC,
(1)证明:∵∠AFB=∠ABC,∠ABC=∠ADC,
∴∠AFB=∠ADC,
∴CD∥BF,
∴∠APD=∠ABF,
∵CD⊥AB,
∴AB⊥BF,
∴直线BF是⊙O的切线.
(2)解:连接OC,
∵CD⊥AB,
∴PD=$\frac{1}{2}$CD,
设OC=OB=x,
∴PB=x-1,
∵tan∠BCD=$\frac{1}{2}$,
∴PC=2(x-1),
在Rt△POC中,OC2=PC2+OP2,
∴x2=(2x-2)2+12,
解得x=$\frac{5}{3}$,x=1(舍去),
∴OB=$\frac{5}{3}$,
∴PD=PC=$\frac{4}{3}$,AB=$\frac{10}{3}$,AP=$\frac{8}{3}$
∵∠PAD=∠BAF,∠APD=∠ABF,
∴△APD∽△ABF,
∴$\frac{AP}{AB}$=$\frac{PD}{BF}$,
∴$\frac{\frac{8}{3}}{\frac{10}{3}}$=$\frac{\frac{4}{3}}{BF}$,
∴BF=$\frac{5}{3}$.
点评 本题考查切线的判定,垂径定理、勾股定理.相似三角形的判定和性质等知识,解题的关键是灵活运用这些知识解决问题,学会条件常用辅助线,属于中考常考题型.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知反比例函数y=$\frac{3}{x}$的图象与正比例函数y=kx(k>0,k≠3),y=3x的图象分别交于A,B,C,D四点.
如图,已知反比例函数y=$\frac{3}{x}$的图象与正比例函数y=kx(k>0,k≠3),y=3x的图象分别交于A,B,C,D四点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
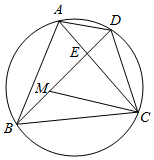 如图,点D是等边三角形ABC外接圆上一点.M是BD上一点,且满足DM=DC,点E是AC与BD的交点.
如图,点D是等边三角形ABC外接圆上一点.M是BD上一点,且满足DM=DC,点E是AC与BD的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com