
 如图,已知反比例函数y=$\frac{3}{x}$的图象与正比例函数y=kx(k>0,k≠3),y=3x的图象分别交于A,B,C,D四点.
如图,已知反比例函数y=$\frac{3}{x}$的图象与正比例函数y=kx(k>0,k≠3),y=3x的图象分别交于A,B,C,D四点.分析 (1)先根据点A的坐标求出k的值,分别列方程组求四个交点的坐标;
(2)根据反比例函数是中心对称图形可知:OA=OB,OC=OD,所以对角线互相平分的四边形是平行四边形,则四边形ACBD是平行四边形;
(3)先列方程组求出点A的坐标,当四边形ACBD是矩形时,OA=OC,根据第1问中点C的坐标利用勾股定理求出OC的长,由OA=OC列式可求得k的值,再求矩形的长和宽,代入面积公式可得矩形面积.
解答 解:(1)把A的坐标为(2,$\frac{3}{2}$)代入y=kx中得:2k=$\frac{3}{2}$,
k=$\frac{3}{4}$,
∴正比例函数解析式为:y=$\frac{3}{4}$x;
由题意得:$\left\{\begin{array}{l}{y=\frac{3}{x}}\\{y=\frac{3}{4}x}\end{array}\right.$ 解得:$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=\frac{3}{2}}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-\frac{3}{2}}\end{array}\right.$,
$\left\{\begin{array}{l}{y=\frac{3}{x}}\\{y=3x}\end{array}\right.$ 解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=3}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=-3}\end{array}\right.$,
∴B(-2,-$\frac{3}{2}$),C(1,3),D(-1,-3);
(2)∵反比例函数y=$\frac{3}{x}$的图象是关于原点O的中心对称图形
∴OA=OB,OC=OD
∴四边形ACBD是平行四边形;
(3)若四边形ACBD是矩形,
∴AB=CD,
∵OA=OB,OC=OD,
∴OC=OA,
∵C(1,3),
∴OA=OC=$\sqrt{10}$,
由$\left\{\begin{array}{l}{y=\frac{3}{x}}\\{y=kx}\end{array}\right.$ 解得:$\left\{\begin{array}{l}{{x}_{1}=\sqrt{\frac{3}{k}}}\\{{y}_{1}=\sqrt{3k}}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=-\sqrt{\frac{3}{k}}}\\{{y}_{2}=-\sqrt{3k}}\end{array}\right.$,
∴A($\sqrt{\frac{3}{k}}$,$\sqrt{3k}$),
∴$(\sqrt{\frac{3}{k}})^{2}+(\sqrt{3k})^{2}$=($\sqrt{10}$)2,
3k2-10k+3=0,
(3k-1)(k-3)=0,
k1=$\frac{1}{3}$,k2=3(舍),
∴正比例函数解析式为:y=$\frac{1}{3}$x;
∴A(3,1),
分别过A、C作x轴、y轴的垂线,交于点E,则△AEC是直角三角形,
AE=3-1=2,CE=3-1=2,
由勾股定理得:AC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{(2\sqrt{10})^{2}-(2\sqrt{2})^{2}}$=4$\sqrt{2}$,
∴S矩形ABCD=BC•AC=4$\sqrt{2}$×$2\sqrt{2}$=16.
点评 本题是四边形与函数的综合题,考查了矩形、平行四边形的性质和判定、一次函数和反比例函数的交点问题,确定两函数交点时,将两函数的解析式列方程组,其解就是交点坐标;同时要熟练掌握矩形、平行四边形的性质和判定;注意数形结合的思想,及坐标与图形的特点.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,C为x轴正半轴上一点,S△ABC=9.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,C为x轴正半轴上一点,S△ABC=9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
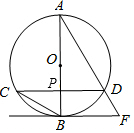 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,点P为AB上一个动点,以DP为折线翻折△APD得到△DPE,A的对应点为点E,连接BE,若AB=3,AD=4,当△BEP为直角三角形时,求AP的长.
如图,在矩形ABCD中,点P为AB上一个动点,以DP为折线翻折△APD得到△DPE,A的对应点为点E,连接BE,若AB=3,AD=4,当△BEP为直角三角形时,求AP的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | msin40° | B. | mcos40° | C. | mtan40° | D. | $\frac{m}{tan40°}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com