[题目]已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示.下面有四个推断:①二次函数y1有最大值,②二次函数y1的图象关于直线x=﹣1对称③当x=﹣2时.二次函数y1的值大于0④过动点P(m.0)且垂直于x轴的直线与y1.y2的图象的交点分别为C.D.当点C位于点D上方时.m的取值范围是m＜﹣3或m＞﹣1 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】已知二次函数y1=ax2+bx+c（a≠0）和一次函数y2=kx+n（k≠0）的图象如图所示，下面有四个推断：

①二次函数y1有最大值；

②二次函数y1的图象关于直线x=﹣1对称

③当x=﹣2时，二次函数y1的值大于0

④过动点P（m，0）且垂直于x轴的直线与y1，y2的图象的交点分别为C，D，当点C位于点D上方时，m的取值范围是m＜﹣3或m＞﹣1．

以上推断正确的是（）

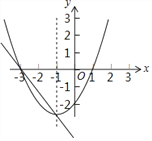
A. ①③ B. ①④ C. ②③ D. ②④

【答案】D

【解析】解：∵二次函数y1=ax2+bx+c（a≠0）的图象的开口向上，∴二次函数y1有最小值，故①错误；

观察函数图象可知二次函数y1的图象关于直线x=﹣1对称，故②正确；

当x=﹣2时，二次函数y1的值小于0，故③错误；

当x＜﹣3或x＞﹣1时，抛物线在直线的上方，∴m的取值范围为：m＜﹣3或m＞﹣1，故④正确．

故选D．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

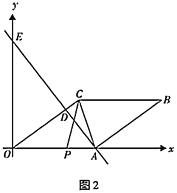
【题目】综合与探究

如图1，在平面直角坐标系中，点是坐标原点，点在轴的正半轴上，点的坐标为，四边形是菱形，直线于点，交轴于点，连接．

（1）点的坐标是______；

（2）求直线的函数解析式；

（3）如图2，动点从点出发，沿折线方向以1个单位长度/秒的速度向终点匀速运动，设的面积为（），点的运动时间为秒，求与之间的函数关系式（要求写出自变量的取值范围）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】叙述并证明三角形内角和定理.

三角形内角和定理： ;

已知：如图△ABC.

求证： .

证明：

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：如图①，在矩形ABCD中，AB=5，AD=，AE⊥BD，垂足是E，点F是点E关于AB的对称点，连接AF、BF

（1）求AE和BE的长；

（2）若将△ABF沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）.当点F分别平移到线段AB、AD上时，直接写出相应的m的值；

（3）如图②，将△ABF绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AD交于点P，与直线BD交于点Q.是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，PQ∥MN，A、B分别为直线MN、PQ上两点，且∠BAN＝45°，若射线AM绕点A顺时针旋转至AN后立即回转，射线BQ绕点B逆时针旋转至BP后立即回转，两射线分别绕点A、点B不停地旋转，若射线AM转动的速度是a°/秒，射线BQ转动的速度是b°/秒，且a、b满足|a﹣5|+（b﹣1）2＝0．（友情提醒：钟表指针走动的方向为顺时针方向）

（1）a＝　　，b＝　　；

（2）若射线AM、射线BQ同时旋转，问至少旋转多少秒时，射线AM、射线BQ互相垂直．

（3）若射线AM绕点A顺时针先转动18秒，射线BQ才开始绕点B逆时针旋转，在射线BQ到达BA之前，问射线AM再转动多少秒时，射线AM、射线BQ互相平行？

查看答案和解析>>

科目：初中数学 来源： 题型：

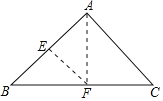
【题目】如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕现交于点F．已知EF=cm，则BC的长是_______________ ．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某学习小组在研究函数y=x3﹣2x的图象与性质时，已列表、描点并画出了图象的一部分．

…

﹣4

﹣3.5

﹣3

﹣2

﹣1

3.5

…

﹣

…

（1）请补全函数图象；

（2）方程x3﹣2x=﹣2实数根的个数为　　；

（3）观察图象，写出该函数的两条性质．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】二次函数y= ax+bx＋c,自变量x 与函数y 的对应值如表:

x	...	－5	－4	－3	－2	－1	0	...
y	...	4	0	－2	－2	0	4	...

下列说法正确的是（）

A. 抛物线的开口向下 B. 当x>-3时，y随x的增大而增大

C. 二次函数的最小值是－2 D. 抛物线的对称轴是x＝－5/2

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知一次函数y=ax+b（a、b是常数，a≠0）函数图象经过（﹣1，4），（2，﹣2）两点，下面说法中：（1）a=2，b=2；（2）函数图象经过（1，0）；（3）不等式ax+b＞0的解集是x＜1；（4）不等式ax+b＜0的解集是x＜1；正确的说法有____________________．（请写出所有正确说法的序号）

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学