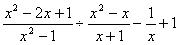练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知y=，试说明在等号右边的代数式有意义的条件下，不论x为何值，y的值不变．
    解：y=
    =    
    =
    =1
    ∴在等号右边的代数式有意义的条件下，不论x为何值，y的值不变.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    24、如图，已知△ABC和△CDE均为等边三角形，且点B、C、D在同一条直线上，连接AD、BE，交CE和AC分别于G、H点，连接GH．
    （1）请说出AD=BE的理由；
    （2）试说出△BCH≌△ACG的理由；
    （3）试猜想：△CGH是什么特殊的三角形，并加以说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    已知：如图，在等边△ABC中，CD是AB边上的高，延长 CB至E，使BE＝BD，连结DE.

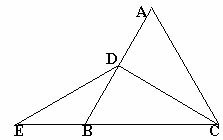
    (1)△CDE是什么三角形？试说明理由；

    (2)把－CD是AB边上的高敻某墒裁刺跫?恳材艿玫酵??慕崧?

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    （1）填空：把下面的推理过程补充完整，并在括号内注明理由．

    已知：如图1，BC∥EF，AB=DE，BC=EF，试说明∠C=∠F．
    解：∵BC∥EF（已知）
    ∴∠ABC=________（________）
    在△ABC与△DEF中

    ∴△ABC≌△DEF（________）
    ∴∠C=∠F（________）
    （2）如图2，A、B、E三点在同一条直线上，△ABC和△BDE都是等边三角形，AD交BC于F，CE分别交BD、AD于G、H，请在图中找出三对全等三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

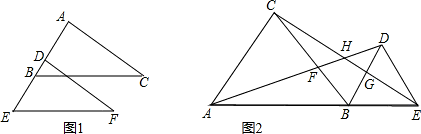
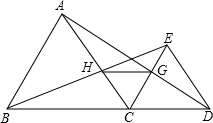    作业宝如图，已知△ABC和△CDE均为等边三角形，且点B、C、D在同一条直线上，连接AD、BE，交CE和AC分别于G、H点，连接GH．
    （1）请说出AD=BE的理由；
    （2）试说出△BCH≌△ACG的理由；
    （3）试猜想：△CGH是什么特殊的三角形，并加以说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    学习《图形的相似》后，我们可以借助探索两个直角三角形全等的条件所获得的经验，继续探索两个直角三角形相似的条件．

    （1）“对于两个直角三角形，满足一边一锐角对应相等，或两直角边对应相等，两个直角三角形全等” ．类似地，你可以等到：“满足                      ，或                               ，两个直角三角形相似” ．

    （2）“满足斜边和一条直角边对应相等的两个直角三角形全等”，类似地你可以得到“满足                             的两个直角三角形相似”。请结合下列所给图形，填出已知中所缺少的条件，并完成说理过程．

    已知：如图，在Ｒt△ABC和Ｒt△A＇B＇C＇中，∠C=∠C=９０°          ．试说明Rt△ABC∽Rt△A’B’C’ ．

    查看答案和解析>>

    同步练习册答案