
 某商家为了给新产品作宜传,向全社会征集广告用语及商标图案,结果如图所示的商标(图中阴影部分)中标,求此商标图案的面积.(虚线左边为扇形,右边为长方形)
某商家为了给新产品作宜传,向全社会征集广告用语及商标图案,结果如图所示的商标(图中阴影部分)中标,求此商标图案的面积.(虚线左边为扇形,右边为长方形) 分析 根据扇形面积公式、长方形面积公式以及三角形面积公式即可求出阴影部分的面积
解答 解:设白色直角三角形的面积为S1,长方形的面积为S2,扇形面积为S3,
∴S3=$\frac{90°π{a}^{2}}{360°}$=$\frac{π{a}^{2}}{4}$
S2=2a×a=2a2,
S1=$\frac{1}{2}$×(2a+a)a=$\frac{3}{2}$a2,
∴S阴影部分=S3+S2-S1
=$\frac{π{a}^{2}}{4}$+2a2-$\frac{3}{2}{a}^{2}$
=$\frac{π{a}^{2}}{4}$+$\frac{{a}^{2}}{2}$
点评 本题考查整式的运算法则,解题的关键是熟练运用扇形面积公式、矩形面积公式,三角形面积公式,本题属于中等题型.


科目:初中数学 来源: 题型:解答题
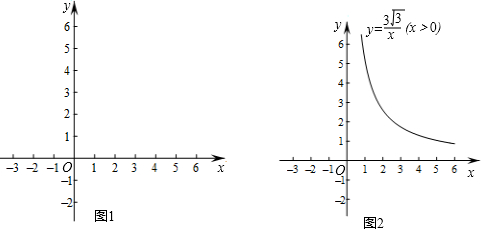
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
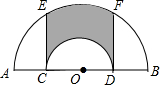 如图,在半圆AOB中,点C为半径OA的中点,以O为圆心,OC为半径画半圆交OB于点D,分别过点C、D作CE、DF垂直AB,交圆O于点E、F,若OA=2,则阴影部分的面积为$\frac{3π}{2}$.
如图,在半圆AOB中,点C为半径OA的中点,以O为圆心,OC为半径画半圆交OB于点D,分别过点C、D作CE、DF垂直AB,交圆O于点E、F,若OA=2,则阴影部分的面积为$\frac{3π}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
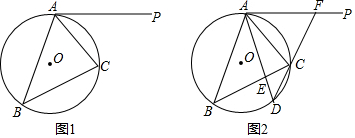
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
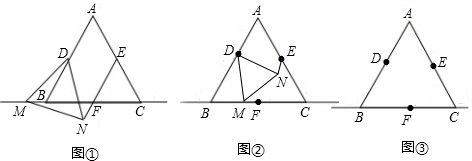
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com