解:(1)∵把△ABC沿直线DE折叠,使△ADE与△BDE重合,
∴∠1=∠A=35°,
∵∠C=90°,
∴∠ABC=180°-90°-35°=55°,
∴∠2=55°-35°=20°,
即∠CBD=20°;
(2)∵把△ABC沿直线DE折叠,使△ADE与△BDE重合,
∴AD=DB,
设CD=x,则AD=BD=4-x,
在Rt△CDB中,CD
2+CB
2=BD
2,
x
2+3
2=(4-x)
2,
解得:x=

,
AD=4-

=3

;
(3)∵△ABC 的面积为m+1,
∴

AC•BC=m+1,
∴AC•BC=2m+2,
∵在Rt△CAB中,CA
2+CB
2=BA
2,
∴CA
2+CB
2+2AC•BC=BA
2+2AC•BC,
∴(CA+BC)
2=m
2+4m+4=(m+2)
2,
∴CA+CB=m+2,
∵AD=DB,
∴CD+DB+BC=m+2.
即△BCD的周长为m+2.
分析:(1)根据折叠可得∠1=∠A=35°,根据三角形内角和定理可以计算出∠ABC=55°,进而得到∠CBD=20°;
(2)根据折叠可得AD=DB,设CD=x,则AD=BD=4-x,再在Rt△CDB中利用勾股定理可得x
2+3
2=(4-x)
2,再解方程可得x的值,进而得到AD的长;
(3)根据三角形ACB的面积可得

AC•BC=m+1,进而得到AC•BC=2m+2,再在Rt△CAB中,CA
2+CB
2=BA
2,再把左边配成完全平方可得CA+CB的长,进而得到△BCD的周长.
点评:此题主要考查了图形的翻折变换,以及勾股定理,完全平方公式,关键是掌握勾股定理,以及折叠后哪些是对应角和对应线段.

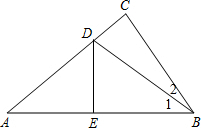
 如图,在△ABC中,∠ACB=90°,若把△ABC沿直线DE折叠,使△ADE与△BDE重合.
如图,在△ABC中,∠ACB=90°,若把△ABC沿直线DE折叠,使△ADE与△BDE重合.
 ,
, =3
=3 ;
; AC•BC=m+1,
AC•BC=m+1, AC•BC=m+1,进而得到AC•BC=2m+2,再在Rt△CAB中,CA2+CB2=BA2,再把左边配成完全平方可得CA+CB的长,进而得到△BCD的周长.
AC•BC=m+1,进而得到AC•BC=2m+2,再在Rt△CAB中,CA2+CB2=BA2,再把左边配成完全平方可得CA+CB的长,进而得到△BCD的周长.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为