
 有趣的问题,太准了!
有趣的问题,太准了!分析 (1)先写出学号的最后一位,再根据操作步骤计算即可求解;
(2)根据六步操作步骤得到代数式,再根据计算法则计算即可求解;
(3)根据操作步骤得到⑤变为把得到的数目加上1768即可求解.
解答 解:(1)我的学号的最后一位是1,
(1×2+5)×50+1766
=(2+5)×50+1766
=7×50+1766
=350+1766
=2116
故操作至第五步,得数是2116.
(2)50(2a+5)+1766
=100a+250+1766
=100a+2016,
故用这个数目减去你出生的那一年,看到的一个三位数(如果少于三位,前面补0凑足三位),第一位数字是你学号的最后一位,接下去就是你的实际年龄;
(3)到了2018年,以上操作不能得到这样的“三位数”.
修改为:⑤把得到的数目加上1766+2=1768.
故答案为:1,2116.
点评 此题考查了有理数的加法,关键是读懂题目的意思,理解题目给出的操作步骤.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
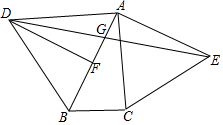 如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABD和△ACE都是等边三角形,F为AB中点,DE交AB于点G
如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABD和△ACE都是等边三角形,F为AB中点,DE交AB于点G查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图.延长线段AB到C,使BC=$\frac{2}{3}$AC.点C是线段BD的中点.
如图.延长线段AB到C,使BC=$\frac{2}{3}$AC.点C是线段BD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
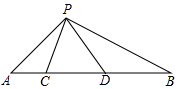 如图,点C、D在线段AB上,且△PCD是边长为1的等边三角形.
如图,点C、D在线段AB上,且△PCD是边长为1的等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com