
【题目】如图,在不等边△ABC中,PM⊥AB于点M,PN⊥AC于点N,且PM=PN,Q在AC上,PQ=QA,MP=3,△AMP的面积是6,下列结论:①AM<PQ+QN,②QP∥AM,③△BMP≌△PQC,④∠QPC+∠MPB=90°,⑤△PQN的周长是7,其中正确的有( )个.

A. 1 B. 2 C. 3 D. 4
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】将连续的奇数1,3,5,7,9,…,排成如图7所示的数阵.
(1)十字框中的五个数的和与中间数15有什么关系?
(2)设中间数为![]() ,用式子表示十字框中五个数之和;
,用式子表示十字框中五个数之和;
(3)若将十字框中上下左右移动,可框住另外五个数,这五个数的和还有这种规律吗?
(4)十字框中五个数之和能等于2005吗?若能,请写出这五个数;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)x2﹣2x﹣8=0;
(2)3x(x﹣1)=2(x﹣1);
(3)x2+3=3(x+1);
(4)2x(4x+5)=7;
(5)4x2﹣8x+1=0;
(6)(y+2)2=(3y﹣1)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)x2﹣2x﹣8=0;
(2)3x(x﹣1)=2(x﹣1);
(3)x2+3=3(x+1);
(4)2x(4x+5)=7;
(5)4x2﹣8x+1=0;
(6)(y+2)2=(3y﹣1)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
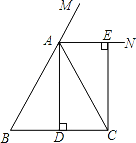
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C. 
(1)求A、B、C三点的坐标.
(2)求抛物线的对称轴及顶点坐标.
(3)抛物线上是否存在点F,使△ABF的面积为1?若存在,求F点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O上有两点A与P,且OA⊥OP,若A点固定不动,P点在圆上匀速运动一周,那么弦AP的长度d与时间t的函数关系的图象可能是( )

A.①
B.③
C.①或③
D.②或④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在数轴上点A表示数a,点B表示数b,且a,b满足![]() .
.
(1)点A表示的数为________,点B表示的数为________;
(2)设点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.若在数轴上存在一点C,使BC=2AC,则点C表示的数为__________;
(3)若在原点处放一挡板,一小球甲从点A处以每秒2个单位长度的速度向左运动;同时另一小球乙从点B以每秒2个单位长度的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)以原来速度的两倍向相反的方向运动.设运动的时间为t秒,请用含t的代数式分别表示出甲、乙两小球到原点的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:

(1)根据上述信息可知:甲命中环数的中位数是 环,乙命中环数的众数是 环;
(2)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会 .(填 “变大”、“变小” 或 “不变”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com