
分析 根据一元二次方程的定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程可得①正确;根据一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件,其中a,b,c分别叫二次项系数,一次项系数,常数项.可得②错误,④正确;把x=1代入3x2+c=0计算可得c=-3,故③错误.
解答 解:①x2=0是一元二次方程,说法正确;
②2x2-1=x是一元二次方程的一般形式,说法错误;
③已知x=1是方程3x2+c=0的根,则c=3,说法错误;
④一元二次方程3x2-3x-1=0的一次项系数是-3,说法正确;
故答案为:①④.
点评 此题主要考查了一元二次方程的一般形式,定义和解,关键是掌握一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 类比三角形中位线的定义,我们给出梯形中位线的定义:如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、DC的中点,称线段EF为梯形ABCD的中位线.
类比三角形中位线的定义,我们给出梯形中位线的定义:如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、DC的中点,称线段EF为梯形ABCD的中位线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=90°,tanB=$\frac{4}{3}$,AC=8,E是AB中点,过点A作直线CD的垂线,垂足为D.
如图,△ABC中,∠ACB=90°,tanB=$\frac{4}{3}$,AC=8,E是AB中点,过点A作直线CD的垂线,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
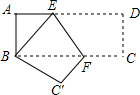 如图,长方形ABCD中,AD=8cm,AB=4cm,沿EF折叠,使点D落到点B处,点C落到点C′处
如图,长方形ABCD中,AD=8cm,AB=4cm,沿EF折叠,使点D落到点B处,点C落到点C′处查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com