
 如图是边长为2的正方形ABCD,对角线为AC,△ABC以点A为中心,顺时针旋转45°得△AB′C′,则图中阴影部分的面积为4$\sqrt{2}$-4.
如图是边长为2的正方形ABCD,对角线为AC,△ABC以点A为中心,顺时针旋转45°得△AB′C′,则图中阴影部分的面积为4$\sqrt{2}$-4. 分析 根据正方形的性质得BC=2,AC=$\sqrt{2}$BC=2$\sqrt{2}$,∠BCA=∠ACD=45°,∠ADC=90°,再利用旋转的性质得∠AC′F=45°,∠FDC′=90°,则FD=DC′,AD=BC=2,则可判断点D在AC上,所以DC′=AC′-DC′=2$\sqrt{2}$-2,易得等腰直角三角形,然后根据等腰直角三角形的性质,利用S阴影部分=S△AB′C′-S△FDC′进行计算.
解答 解:∵四边形ABCD为正方形,
∴BC=2,AC=$\sqrt{2}$BC=2$\sqrt{2}$,∠BCA=∠ACD=45°,∠ADC=90°,
∵△ABC以点A为中心,顺时针旋转45°得△AB′C′,
∴∠AC′B′=45°,∠FDC′=∠FDA=90°,AD=BC=2,
∴点G在BD上,
∴DC′=AC′-AD=2$\sqrt{2}$-2,
∵△DFG为等腰直角三角形,
∴DF=DC′=2$\sqrt{2}$-2,
∴S阴影部分=S△AB′C′-S△FDC′=$\frac{1}{2}$×2×2-$\frac{1}{2}$×(2$\sqrt{2}$-2)2=4$\sqrt{2}$-4.
故答案为4$\sqrt{2}$-4.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
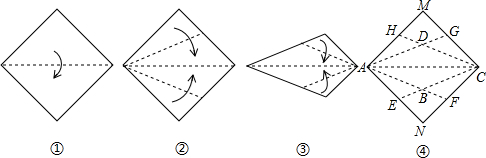 在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形,把一张正方形纸片按照图①~④的过程折叠后展开.
在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形,把一张正方形纸片按照图①~④的过程折叠后展开.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=4,ED=8.
如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=4,ED=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD=120°,AM=AN=$\sqrt{3}$,
如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD=120°,AM=AN=$\sqrt{3}$,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com