
【题目】已知关于x的一元二次方程![]() .
.
(1)求证:无论k取何实数值,方程总有实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c恰好是这个方程的两个根,求此三角形的三边长?
【答案】(1)见解析;(2)三角形的三边为4、6、6或6、6、10.
【解析】
(1)计算方程的判别式大于等于0即可;
(2)由等腰三角形的性质有a=b=6、a=c=6或b=c三种情况,当b=6或c=6时,可知x=2为方程的一个根,代入可求得k的值,则可求得方程的根,可求得三边长;当b=c时,可知方程有两个相等的实数根,由判别式等于0可求得k,同样可求得方程的两根,可求得三角形的三边长.
(1)证明:
∵一元二次方程x2﹣(3k+1)x+2k2+2k=0,
∴△=(3k+1)2﹣4(2k2+2k)=9k2+6k+1﹣8k2+8k=k2﹣2k+1=(k﹣1)2≥0,
∴无论k取何实数值,方程总有实数根;
(2)解:
∵△ABC为等腰三角形,
∴有a=b=6、a=c=6或b=c三种情况,
①当a=b=6或a=c=6时,可知x=6为方程的一个根,
∴62﹣6(3k+1)+2k2+2k=0,解得k=3或k=5,
当k=3时,方程为x2﹣10x+24=0,解得x=4或x=6,
∴三角形的三边长为4、6、6,
当k=5时,方程为x2﹣16x+60=0,解得x=6或x=10,
∴三角形的三边长为6、6、10,
②当b=c时,则方程有两个相等的实数根,
∴△=0,即(k﹣1)2=0,解得k1=k2=1,
∴方程为x2﹣4x+4=0,解得x1=x2=2,
此时三角形三边为6、2、2,不满足三角形三边关系,舍去,
综上可知三角形的三边为4、6、6或6、6、10.


科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:若存在实数![]() ,对于函数图象上横坐标之差为1的任意两点
,对于函数图象上横坐标之差为1的任意两点![]() ,
,![]() ,
,![]() 都成立,则称这个函数是限减函数,在所有满足条件的
都成立,则称这个函数是限减函数,在所有满足条件的![]() 中,其最大值称为这个函数的限减系数.例如,函数
中,其最大值称为这个函数的限减系数.例如,函数![]() ,当
,当![]() 取值
取值![]() 和
和![]() 时,函数值分别为
时,函数值分别为![]() ,
,![]() ,故
,故![]() ,因此函数
,因此函数![]() 是限减函数,它的限减系数为
是限减函数,它的限减系数为![]() .
.
(1)写出函数![]() 的限减系数;
的限减系数;
(2)![]() ,已知
,已知![]() (
(![]() )是限减函数,且限减系数
)是限减函数,且限减系数![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)已知函数![]() 的图象上一点
的图象上一点![]() ,过点
,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,将函数
轴,将函数![]() 的图象在点
的图象在点![]() 右侧的部分关于直线
右侧的部分关于直线![]() 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数
翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数![]() ,直接写出
,直接写出![]() 点横坐标
点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
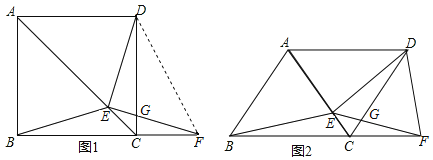
【题目】如图1,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 交
交![]() 于
于![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() ,求
,求![]() ;
;
(3)如图2,若把正方形![]() 改为菱形
改为菱形![]() ,其他条件不变,当
,其他条件不变,当![]() 时,猜想
时,猜想![]() 与
与![]() 的数量关系,并证明你的猜想.
的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
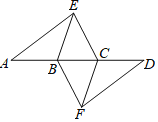
【题目】如图,点A、B、C、D依次在同一条直线上,点E、F分别在直线AD的两侧,已知BE∥CF,∠A=∠D,AE=DF.
(1)求证:四边形BFCE是平行四边形;
(2)填空:若AD=7,AB=2.5,∠EBD=60°,当四边形BFCE是菱形时,菱形BFCE的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
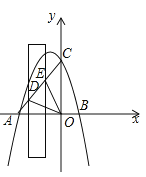
【题目】如图,抛物线![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为( )
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.
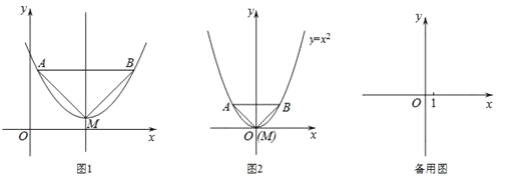
(1)①如图2,求出抛物线y=x2的“完美三角形”斜边AB的长;
②请写出一个抛物线的解析式,使它的完美三角形与y=x2+1的“完美三角形”全等;
(2)若抛物线y=ax2+4的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线y=mx2+2x+n5的“完美三角形”斜边长为n,且y=mx2+2x+n5的最大值为1,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
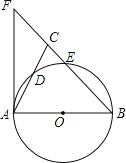
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区![]() 号楼对外销售,已知
号楼对外销售,已知![]() 号楼某单元共
号楼某单元共![]() 层,一楼为商铺,只租不售,二楼以上价格如下:第
层,一楼为商铺,只租不售,二楼以上价格如下:第![]() 层售价为
层售价为![]() 元/米
元/米![]() ,从第
,从第![]() 层起每上升一层,每平方米的售价提高
层起每上升一层,每平方米的售价提高![]() 元,反之每降一层,每平方米的售价降低
元,反之每降一层,每平方米的售价降低![]() 元,已知该单元每套的面积均为
元,已知该单元每套的面积均为![]() 米
米![]()
优惠活动
活动一:若一次性付清所有房款,降价![]() ,另免
,另免![]() 年物业费共
年物业费共![]() 元.
元.
活动二:若购买者一次性付清所有房款,降价![]() ,无赠送.
,无赠送.
(1)请在下表中,补充完整售价![]() (元/米
(元/米![]() )与楼层
)与楼层![]() (
(![]() 取正整数)之间的的数关系式.
取正整数)之间的的数关系式.
楼层 |
|
|
|
|
售价 | 不售 |
|
(2)某客户想购买该单元第![]() 层的一套楼房,若他一次性付清购房款,可以参加如图优惠活动.请你帮助他分析哪种优惠方案更合算
层的一套楼房,若他一次性付清购房款,可以参加如图优惠活动.请你帮助他分析哪种优惠方案更合算

查看答案和解析>>
科目:初中数学 来源: 题型:
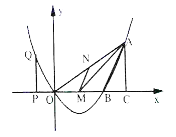
【题目】如图,二次函数的图象经过原点![]() 和
和![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,且对称轴是
,且对称轴是![]() .
.
(1)求二次函数的表达式;
(2)若![]() 是
是![]() 上的一点,作
上的一点,作![]() ,交
,交![]() 于点
于点![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)![]() 是
是![]() 轴上的点,过
轴上的点,过![]() 作
作![]() 轴,与抛物线交于点
轴,与抛物线交于点![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,是否存在点
,是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形与以点
为顶点的三角形与以点![]() 、
、![]() 、
、![]() 为顶点的三角形相似?若存在,求出点
为顶点的三角形相似?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com