
把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为

5.
【解析】
试题分析:由题意,⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧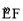 于点H、I,再连接OF,易求得FH的长,然后设求半径为r,则OH=16﹣r,然后在Rt△OFH中,r2﹣(16﹣r)2=82,解此方程即可求得答案:
于点H、I,再连接OF,易求得FH的长,然后设求半径为r,则OH=16﹣r,然后在Rt△OFH中,r2﹣(16﹣r)2=82,解此方程即可求得答案:
如答图,由题意,⊙O与BC相切,记切点为M,作直线OM,分别交AD、劣弧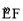 于点H、N,再连接OF,
于点H、N,再连接OF,
在矩形ABCD中,AD∥BC,而MN⊥BC,∴MN⊥AD.∴在⊙O中,FH=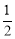 EF=4.
EF=4.
设球半径为r,则OH=8﹣r,
在Rt△OFH中,由勾股定理得,r2﹣(8﹣r)2=42,解得r=5.
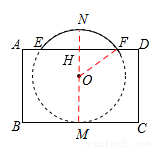
考点:1.垂径定理的应用;2.勾股定理;3.切线的性质;4.方程思想的应用.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源:2014年初中毕业升学考试(广东深圳卷)数学(解析版) 题型:选择题
二次函数y=ax2+bx+c图象如图,下列正确的个数为( )
①bc>0;
②2a﹣3c<0;
③2a+b>0;
④ax2+bx+c=0有两个解x1,x2,x1>0,x2<0;
⑤a+b+c>0;
⑥当x>1时,y随x增大而减小.

A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)当动点P在直线OB上时,点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,求PA:PC的值.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:选择题
如图,圆锥的侧面展开图使半径为3,圆心角为90°的扇形,则该圆锥的底面周长为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(海南卷)数学(解析版) 题型:选择题
将抛物线y=x2平移得到抛物线y=(x+2)2,则这个平移过程正确的是( )
A.向左平移2个单位 B.向右平移2个单位
C.向上平移2个单位 D.向下平移2个单位
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级上册第九章9.3整式的乘法练习卷(解析版) 题型:选择题
计算(﹣a)2•a3的结果是( )
A.a5 B.a6 C.﹣a5 D.﹣a6
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学七年级上册第九章9.3积的乘方练习卷(解析版) 题型:选择题
计算(﹣2a3)2的结果是( )
A.2a5 B.4a5 C.﹣2a6 D.4a6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com