Question

如图，在平面直角坐标系中，直线l平行x轴，交y轴于点A，第一象限内的点B在l上，连结OB，动点P满足∠APQ=90°，PQ交x轴于点C．

（1）当动点P与点B重合时，若点B的坐标是（2，1），求PA的长．

（2）当动点P在线段OB的延长线上时，若点A的纵坐标与点B的横坐标相等，求PA：PC的值．

（3）当动点P在直线OB上时，点D是直线OB与直线CA的交点，点E是直线CP与y轴的交点，若∠ACE=∠AEC，PD=2OD，求PA：PC的值．

 

 

Answer 1

（1）2；（2）1：1；（3）或．

【解析】

试题分析：（1）易得点P的坐标是（2，1），即可得到PA的长．

（2）易证∠AOB=45°，由角平分线的性质可得PA=PC，然后通过证明△ANP≌△CMP即可求出PA：PC的值．

（3）可分点P在线段OB的延长线上及其反向延长线上两种情况进行讨论．易证PA：PC=PN：PM，设OA=x，只需用含x的代数式表示出PN、PM的长，即可求出PA：PC的值．

试题解析：【解析】
（1）∵点P与点B重合，点B的坐标是（2，1），∴点P的坐标是（2，1）．∴PA的长为2．

（2）如答图1，过点P作PM⊥x轴，垂足为M，过点P作PN⊥y轴，垂足为N，

∵点A的纵坐标与点B的横坐标相等，∴OA=AB．

∵∠OAB=90°，∴∠AOB=∠ABO=45°．

∵∠AOC=90°，∴∠POC=45°．

∵PM⊥x轴，PN⊥y轴，∴PM=PN，∠ANP=∠CMP=90°．∴∠NPM=90°．

∵∠APC=90°．∴∠APN=90°﹣∠APM=∠CPM．

在△ANP和△CMP中，∵∠APN=∠CPM，PN=PM，∠ANP=∠CMP，

∴△ANP≌△CMP．∴PA=PC．∴PA：PC的值为1：1．

（3）①若点P在线段OB的延长线上，如答图2，过点P作PM⊥x轴，垂足为M，过点P作PN⊥y轴，垂足为N，PM与直线AC的交点为F．

∵∠APN=∠CPM，∠ANP=∠CMP，∴△ANP∽△CMP．∴．

∵∠ACE=∠AEC，∴AC=AE．

∵AP⊥PC，∴EP=CP．

∵PM∥y轴，∴AF=CF，OM=CM．∴FM=OA．

设OA=x，∵PF∥OA，∴△PDF∽△ODA．∴.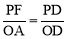

∵PD=2OD，∴PF=2OA=2x，FM=x．∴PM=x．

∵∠APC=90°，AF=CF，∴AC=2PF=4x．

∵∠AOC=90°，∴OC=x．

∵∠PNO=∠NOM=∠OMP=90°，∴四边形PMON是矩形．∴PN=OM=x．

∴PA：PC=PN：PM=x：x=．

②若点P在线段OB的反向延长线上，如答图3，过点P作PM⊥x轴，垂足为M，过点P作PN⊥y轴，垂足为N，PM与直线AC的交点为F．

同理可得：PM=x，CA=2PF=4x，OC=x．

∴PN=OM=OC=x．

∴PA：PC=PN：PM=x：x=．

综上所述：PA：PC的值为或．

考点：1.单动点问题；2.全等三角形的判定和性质；3.角平分线的性质；4.等腰三角形的判定和性质；5.勾股定理；6.矩形的判定和性质；7.平行线分线段成比例；8.相似三角形的判定和性质；9.分类思想的应用．