
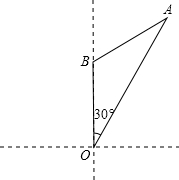
 如图,我国海监船在O处观测到一日系船正匀速直线航行我国海域,当该日系船位于点O的北偏东30°方向上的点A处(OA=20
如图,我国海监船在O处观测到一日系船正匀速直线航行我国海域,当该日系船位于点O的北偏东30°方向上的点A处(OA=20| 3 |
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
 (2013•宝安区一模)钓鱼岛自古以来是中国领土,如图,我国海监船正在钓鱼岛A附近海域执法,当巡航至B处时,得知正东方向的C处有一艘渔船出故障,于是我海监船立刻以25海里/小时向正东方向进行救援.已知钓鱼岛A位于B处的北偏东30°方向上,钓鱼岛A位于C处的北偏东45°方向上,且AB=20
(2013•宝安区一模)钓鱼岛自古以来是中国领土,如图,我国海监船正在钓鱼岛A附近海域执法,当巡航至B处时,得知正东方向的C处有一艘渔船出故障,于是我海监船立刻以25海里/小时向正东方向进行救援.已知钓鱼岛A位于B处的北偏东30°方向上,钓鱼岛A位于C处的北偏东45°方向上,且AB=20| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=45海里,OB=15海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
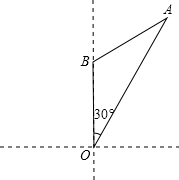 如图,我国海监船在O处观测到一日系船正匀速直线航行我国海域,当该日系船位于点O的北偏东30°方向上的点A处(OA=20
如图,我国海监船在O处观测到一日系船正匀速直线航行我国海域,当该日系船位于点O的北偏东30°方向上的点A处(OA=20 km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测得该日系船位于点O的正北方向上的点B处,且OB=20km,求该日系船航行的速度.
km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测得该日系船位于点O的正北方向上的点B处,且OB=20km,求该日系船航行的速度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
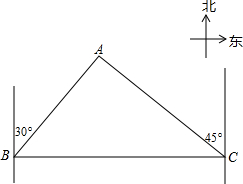 钓鱼岛自古以来是中国领土,如图,我国海监船正在钓鱼岛A附近海域执法,当巡航至B处时,得知正东方向的C处有一艘渔船出故障,于是我海监船立刻以25海里/小时向正东方向进行救援.已知钓鱼岛A位于B处的北偏东30°方向上,钓鱼岛A位于C处的北偏东45°方向上,且AB=20
钓鱼岛自古以来是中国领土,如图,我国海监船正在钓鱼岛A附近海域执法,当巡航至B处时,得知正东方向的C处有一艘渔船出故障,于是我海监船立刻以25海里/小时向正东方向进行救援.已知钓鱼岛A位于B处的北偏东30°方向上,钓鱼岛A位于C处的北偏东45°方向上,且AB=20 海里.
海里. =1.732,结果要精确到0.1)
=1.732,结果要精确到0.1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com