
����Ŀ��һ����������������ԭ��������������ϵ�һ��һ��������������һ�����������������ľ�������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��1�����![]() ������������ô��
������������ô��![]() �������ľ�����______��
�������ľ�����______��
��2����![]() �����������λ������Ӧ����������______��
�����������λ������Ӧ����������______��
��3����![]() ������������λ����ԭ���______�ࣻ
������������λ����ԭ���______�ࣻ
��4��������ڳ����㣬���������һ��������![]() �������������ڶ���������
�������������ڶ���������![]() �������������Դ����ƣ����
�������������Դ����ƣ����![]() ������������ô��
������������ô��![]() �μ���______��
���______��
�ڻ���������������������λ����ԭ���ͬ�ࣿ
���𰸡���1��n����2��-3����3���ң���4����![]() ���ڲ��ᣬ������
���ڲ��ᣬ������
��������
��1����������ɵõ�n�������ľ���Ϊn����2��������ʽ-1+2-3+4-5= -3�ɵã���3��������ʽ-1+2-3+4-5+��+100= 50�ɵã���4���ٸ����桢ż���ı�ʾ�����ɵã�����ʽ���㣬���ݼ����������ж�.
�⣺��1���ߵ�һ�����������Ĵ������ľ���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��
���n�������ľ���Ϊ![]() ��
��
��2����������ã�![]() ��
��
���![]() �����������λ������Ӧ����������-3��
�����������λ������Ӧ����������-3��
��3����������ã�![]() ��
��
���![]() ������������λ����ԭ����Ҳࣻ
������������λ����ԭ����Ҳࣻ
��4���ٸ�������ɵã���n��nΪ��������Ϊ����ʱ����ԭ����࣬��Ϊn���෴��-n����n��nΪ��������Ϊż��ʱ����ԭ���Ҳ࣬��Ϊn��
�൱![]() ������������
������������![]() ���
���![]() .
.
�ڲ���
��ͣ�![]()
��![]() Ϊ����ʱ��ԭʽ
Ϊ����ʱ��ԭʽ![]()
��![]() Ϊż��ʱ��ԭʽ
Ϊż��ʱ��ԭʽ![]()
�ɴ˿�֪��������������ÿ����һ���������͵ķ��Ŷ���ı䣬�ʲ�����������������������λ����ԭ���ͬ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣���ͼ��ʾ�����ı���ABCD�У�AB=2![]() ��BC=2��CD=1��AD=5���ҡ�C=90�������ı���ABCD�����.
��BC=2��CD=1��AD=5���ҡ�C=90�������ı���ABCD�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ٵ��ˣ�����ӭ���ֻ��г�������������ij�̳����ۼס�������Ʒ�Ƶ������ֻ����������ֻ��Ľ��ۺ��ۼ����±���ʾ��
�� | �� | |
���ۣ�Ԫ/���� | 4000 | 2500 |
�ۼۣ�Ԫ/���� | 4300 | 3000 |
���̳��ƻ�Ͷ��15.5��Ԫ�ʽ�ȫ�����ڹ��������ֻ����ɲ�������ȫ�����ۺ�ɻ�ë������2��Ԫ����ë����=���ۼ۩����ۣ�����������
��1�����̳�Ҫ�뾡���ܶ�Ĺ��������ֻ���Ӧ�ð��������Ľ��������������������ֻ���
��2��ͨ���г����У����̳������ڼ����ֻ��������ķ����ϣ����ټ����ֻ��Ĺ������������������ֻ��Ĺ�����������֪�����ֻ����ӵ������Ǽ����ֻ����ٵ�������2�����������ڹ����������ֻ������ʽ���16��Ԫ�����̳�����������ʹȫ�����ۺ��õ�ë�������������ë����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A���������ϱ�ʾ����Ϊ��16��AB�������50����λ���ȣ�С����A�س���ȥB�أ���ÿ����2����λ���ȵ��ٶ��н�����һ��������1��λ���ȣ��ڶ�������2��λ���ȣ�������������3��λ���ȣ����Ĵ�������4��λ�����������˹����н���
![]()
��1�����B���������ϱ�ʾ������
��2����B����ԭ����Ҳ࣬������8���н���С�������P����ʱ��P���B��༸����λ���ȣ�8���˶���ɺ�һ�������˼����ӣ�
��3��������n�Σ�nΪ���������н���С�������Q������ֱ��д������Q�������ϱ�ʾ����Ӧ��α�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����걾���۽۴������ijˮ��������һ���۽����ɱ���Ϊ10Ԫ/ǧ������֪���ۼ۲����ڳɱ���������۲��Ź涨���ֲ�Ʒ�����ۼ۲�����18Ԫ/ǧ�����г����鷢�����ò�Ʒÿ���������y��ǧ���������ۼ�x��Ԫ/ǧ����֮��ĺ�����ϵ��ͼ��ʾ��
��1����y��x֮��ĺ�����ϵʽ��
��2���þ�������Ҫÿ����150Ԫ���������������ۼ�Ӧ��Ϊ������
����������=���ۼ����ɱ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD������֪AB=6��BC=9�� ![]() ���Խ���AC��BD���ڵ�O������P�ڱ�AB������P������B�����߶�PA�ڵ�E����BP= x��
���Խ���AC��BD���ڵ�O������P�ڱ�AB������P������B�����߶�PA�ڵ�E����BP= x��
��1����AC�ij���
��2������O�İ뾶Ϊy������P����O����ʱ����y����x�ĺ�������ʽ����д����������
��3�����AC����O��ֱ������O������E������O����P��Բ�ľ�OP�ij���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A������Ϊ����2��0������B������Ϊ��0��n�����Ե�BΪֱ�Ƕ��㣬��C�ڵڶ������ڣ�������ֱ����ABC��
��1����C������Ϊ ������ĸn��ʾ��
��2�������ABC�����Ϊ5.5����n��ֵ��
��3���ڣ�2���������£�����ƽ�����Ƿ����һ��M��ʹ�Ե�M��A��BΪ������ɵ�����������ABCȫ�ȣ�������ڻ�������Ҫ���ͼ�Σ������M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ��O��OE�ǡ�AOC��ƽ���ߣ�OF��CD��OG��OE����BOD=52����
��1�����AOC����AOF�Ķ�����
��2�����EOF���BOG�Ƿ���ȣ���˵�����ɣ�
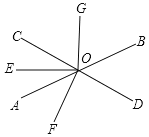
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ı���ABCD�Ǿ���,��E��CD����,��F��DC�ӳ�����,AE=BF��
��1����֤���ı���ABFE��ƽ���ı��Σ�
��2������BEF=��DAE,AE=3,BE=4,��EF�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com