【题目】下列下列命题是真命题的是（ ）
A. 过一点有且只有一条直线与已知直线垂直
B. 相等的两个角一定是对顶角
C. 将一根细木条固定在墙上，只需要一根钉子
D. 同角的余角相等
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO.若∠COB＝60°，FO＝FC，则下列结论：①FB⊥OC，OM＝CM；②△EOB≌△CMB；③四边形EBFD是菱形；④MB∶OE＝3∶2.其中正确结论的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，延长⊙O的直径AB至点C，使得BC=
AB，点P是⊙O上半部分的一个动点（点P不与A、B重合），连结OP，CP．
（1）∠C的最大度数为 ；
（2）当⊙O的半径为3时，△OPC的面积有没有最大值？若有，说明原因并求出最大值；若没有，请说明理由；
（3）如图2，延长PO交⊙O于点D，连结DB，当CP=DB时，求证：CP是⊙O的切线．
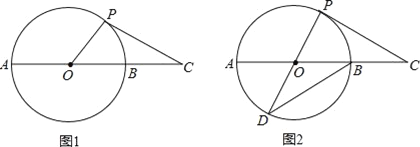
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，有长为24m的篱笆，围成中间隔有一道篱笆的长方形的花圃，且花圃的长可借用一段墙体(墙体的最大可用长度a＝10m)．
(1)如果所围成的花圃的面积为45m2，试求宽AB的长；
(2)按题目的设计要求，能围成面积比45m2更大的花圃吗?如果能，请求出最大面积，并说明围法；如果不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的边长是4，∠DAC的角平分线交DC于点E，点P、Q分别是边AD和AE上的动点（两动点不重合）．
（1）PQ+DQ的最小值是 ．
（2）说出PQ+DQ取得最小值时，点P、Q的位置，并在图中画出；
（3）请对（2）中你所给的结论进行证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．
（1）请写出图2中阴影部分的面积；
（2）观察图2你能写出下列三个代数式之间的等量关系吗？
代数式：（m+n）2， （m﹣n）2， mn；
（3）根据（2）中的等量关系，解决如下问题：若a+b=7，ab=5，求（a﹣b）2的值．
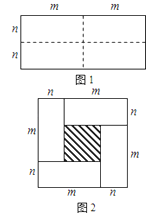
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平行四边形ABCD中，AB⊥AC，AB=1，BC=
．对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F．
（1）证明：当旋转角为90°时，四边形ABEF是平行四边形；
（2）试说明在旋转过程中，线段AF与EC总保持相等；
（3）在旋转过程中，四边形BEDF可能是菱形吗？如果不能，请说明理由；如果能，说明理由并求出此时AC绕点O顺时针旋转的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
