
如图,抛物线![]() 与
与![]() 关于
关于![]() 轴对称,顶点分别为B、A,
轴对称,顶点分别为B、A,![]() 与
与![]() 轴的交点为C. 若由A,B,C组成的三角形中,
轴的交点为C. 若由A,B,C组成的三角形中,![]() . 求:
. 求:
(1)![]() 满足的关系式;
满足的关系式;
(2)如图,动点Q、M分别在![]() N、P在
N、P在![]() 轴上,构成矩形MNPQ,当
轴上,构成矩形MNPQ,当![]() 为1时,请问:
为1时,请问:
①Q点坐标是多少时,矩形MNPQ的周长最短?
②若E为MQ与![]() 轴的交点,是否存在这样的矩形,使得△CEQ与△QPB相似?若存在,请直接写出Q点坐标;若不存在,请说明理由.
轴的交点,是否存在这样的矩形,使得△CEQ与△QPB相似?若存在,请直接写出Q点坐标;若不存在,请说明理由.
|
(第23题) |
科目:初中数学 来源: 题型:解答题
 与x轴的两个交点A、B,与y轴交于点C,A点坐标为(
与x轴的两个交点A、B,与y轴交于点C,A点坐标为(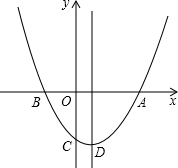 4,0),C点坐标(0,-4).
4,0),C点坐标(0,-4).查看答案和解析>>
科目:初中数学 来源: 题型:
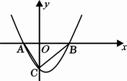
如图,抛物线![]() 与x轴交于A,B两点,与y轴交于点C,其顶点在直线y=-2x上.
与x轴交于A,B两点,与y轴交于点C,其顶点在直线y=-2x上.
(1)求a的值;
(2)求A,B两点的坐标;
(3)以AC,CB为一组邻边作□ACBD,则点D关于x轴的对称点D´是否在该抛物线上?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(广东汕头卷)数学(带解析) 题型:解答题
如图,抛物线 与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
与x轴交于A、B两点,与y轴交于点C,连接BC、AC.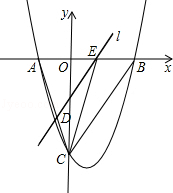
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(湖南张家界卷)数学(带解析) 题型:解答题
如图,抛物线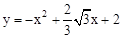 与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
(1)分别求出点A.点B的坐标;
(2)求直线AB的解析式;
(3)若反比例函数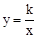 的图象过点D,求k值;
的图象过点D,求k值;
(4)两动点P、Q同时从点A出发,分别沿AB.AO方向向B.O移动,点P每秒移动1个单位,点Q每秒移动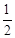 个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2009年江苏省泰州市(姜堰市二附中等)四所名校中考数学二模试卷(解析版) 题型:解答题
 与x轴的两个交点A、B,与y轴交于点C,A点坐标为(4,0),C点坐标(0,-4).
与x轴的两个交点A、B,与y轴交于点C,A点坐标为(4,0),C点坐标(0,-4).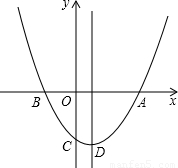
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com