
【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是______.

【答案】34
【解析】
由正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出四边形EFGH是正方形,由勾股定理得EH,即可得出正方形EFGH的面积.
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG.
在△AEH、△BFE、△CGF和△DHG中,

∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形,
∵AB=BC=CD=DA=8,AE=BF=CG=DH=5,
∴EH=FE=GF=GH=![]()
所以正方形EFGH的面积![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某体育用品商店购进乒乓球拍和羽毛球拍进行销售,已知羽毛球拍比乒乓球拍每副进价高20元,用10000元购进羽毛球拍与用8000元购进乒乓球拍的数量相等.
(1)求每副乒乓球拍、羽毛球拍的进价各是多少元?
(2)该体育用品商店计划用不超过8840元购进乒乓球拍、羽毛球拍共100副进行销售,且乒乓球拍的进货量不超过60副,请求出该商店有几种进货方式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=![]() x+
x+![]() 与y轴的交点为A,直线l1与直线l2:y=kx的交点M的坐标为M(3,a).
与y轴的交点为A,直线l1与直线l2:y=kx的交点M的坐标为M(3,a).
⑴a= ,k= ;
⑵直接写出关于x的不等式![]() x+
x+![]() ≥kx>0的解集 ;
≥kx>0的解集 ;
⑶若点B在x轴上,MB=MA,直接写出点B的坐标 .
⑷在x轴上是否存在一点N,使得NM-NA的值最大,若不存在,请说明理由;若存在,请直接写出点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
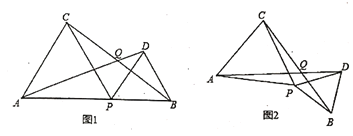
【题目】如图1,点![]() 是线段
是线段![]() 上的动点(点
上的动点(点![]() 与
与![]() 不重合),分别以
不重合),分别以![]() 为边向线段
为边向线段![]() 的同一侧作正
的同一侧作正![]() 和正
和正![]() .
.
(1)请你判断![]() 与
与![]() 有怎样的数量关系?请说明理由;
有怎样的数量关系?请说明理由;
(2)连接![]() ,相交于点
,相交于点![]() ,设
,设![]() ,那么
,那么![]() 的大小是否会随点
的大小是否会随点![]() 的移动而变化?请说明理由;
的移动而变化?请说明理由;
(3)如图2,若点![]() 固定,将
固定,将![]() 绕点
绕点![]() 按顺时针方向旋转(旋转角小于
按顺时针方向旋转(旋转角小于![]() ),此时
),此时![]() 的大小是否发生变化?(只需直接写出你的猜想,不必证明)
的大小是否发生变化?(只需直接写出你的猜想,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列四项调查中,方式正确的是![]()
![]()
A. 了解本市中学生每天学习所用的时间,采用全面调查的方式
B. 为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式
C. 了解某市每天的流动人口数,采用全面调查的方式
D. 了解全市中学生的视力情况,采用抽样调查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b和反比例函数y2=![]() 的图象交于A、B两点.
的图象交于A、B两点.

(1)求一次函数y1=kx+b和反比例函数y2=![]() 的解析式;
的解析式;
(2)观察图象写出y1<y2时,x的取值范围为 ;
(3)求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某街道1000米的路面下雨时经常严重积水.需改建排水系统.市政公司准备安排甲、乙两个工程队做这项工程,根据评估,有两个施工方案:
方案一:甲、乙两队合作施工,那么12天可以完成;
万案二:如果甲队先做10天,剩下的工程由乙队单独施工,还需15天才能完成.
(l)甲、乙两队单独完成此项工程各需多少天?
(2)方案一中,甲、乙两队实际各施工了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海滨浴场东西走向的海岸线可以近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号,他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲乙的游泳速度都是2米/秒.问谁先到达B处?请说明理由.
(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com