
【题目】如图,一次函数y1=kx+b和反比例函数y2=![]() 的图象交于A、B两点.
的图象交于A、B两点.

(1)求一次函数y1=kx+b和反比例函数y2=![]() 的解析式;
的解析式;
(2)观察图象写出y1<y2时,x的取值范围为 ;
(3)求△OAB的面积.
【答案】(1)一次函数的解析式是:y1=![]() x﹣
x﹣![]() ;反比例函数的解析式是:y2=
;反比例函数的解析式是:y2=![]() ;
;
(2)x<﹣2或0<x<3;(3)![]() .
.
【解析】
试题分析:(1)根据图形得出A、B的坐标,把A的坐标代入反比例函数的解析式,即可求出其解析式;把A、B的坐标代入一次函数的解析式,即可求出一次函数的解析式;
(2)根据图象和A、B的横坐标,即可得出答案.
(3)求得直线与y轴的交点,然后根据三角形面积公式即可求得.
试题解析:(1)由图可知:A(﹣2,﹣2),
∵反比例函数y2=![]() 的图象过点A(﹣2,﹣2),
的图象过点A(﹣2,﹣2),
∴m=4,
∴反比例函数的解析式是:y2=![]() ,
,
把x=3代入得,y=![]() ,
,
∴B(3,![]() ),
),
∵y=kx+b过A、B两点,
∴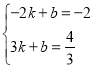
解得:k=![]() ,b=﹣
,b=﹣![]() ,
,
∴一次函数的解析式是:y1=![]() x﹣
x﹣![]() ;
;
(2)根据图象可得:当x<﹣2或0<x<3时,y1<y2.
故答案为x<﹣2或0<x<3.
(3)由一次函数y1=![]() x﹣
x﹣![]() 可知直线与y轴的交点为(0,﹣
可知直线与y轴的交点为(0,﹣![]() ),
),
∴△OAB的面积=![]() ×
×![]() ×2+
×2+![]() ×
×![]() ×3=
×3=![]() .
.


科目:初中数学 来源: 题型:
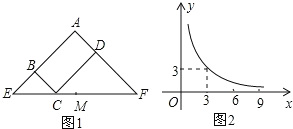
【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的序号是___.①当x=3时,EC<EM;②当y=9时,EC>EM③当x增大时,ECCF的值增大;④当y增大时,BEDF的值不变。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市“青山绿水”行动中,某社区计划对面积为![]() 的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为
的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为![]() 区域的绿化时,甲队比乙队少用6天.
区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天各能完成多少面积的绿化;
(2)若甲队每天绿化费用是1.2万元,乙队每天绿化费用为0.5万元,社区要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
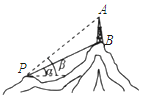
【题目】在一山顶有铁塔AB,从点P到铁塔底部B点有一条索道PB,索道长为300米,与水平线成角为α=30°,在P处测得A点的仰角为β=45°,试求铁塔的高AB.(精确到0.1米,其中![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有甲、乙两个小分队分别同时从B、C两地出发前往A地,甲沿线路BA行进,乙沿线路CA行进,已知C在A的南偏东55°方向,AB的坡度为1:5,同时由于地震原因造成BC路段泥石堵塞,在BC路段中位于A的正南方向上有一清障处H,负责抢修BC路段,已知BH为12000m.
(1)求BC的长度;
(2)如果两个分队在前往A地时匀速前行,且甲的速度是乙的速度的三倍.试判断哪个分队先到达A地.(tan55°≈1.4,sin55°≈0.84,cos55°≈0.6,![]() ≈5.01,结果保留整数)
≈5.01,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将一根绳子平放在桌上,用剪刀任意剪n刀(如图①),绳子变成n+1段;若将绳子对折1次后从中间剪一刀(如图②),绳子的刀口 个,绳子变成 段;若将绳子对折2次后从中间剪一刀,绳子的刀口有 个,绳子变成 段;若将绳子对折n次后从中间剪一刀,绳子的刀口 个,绳子变成 段.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com