
【题目】如图,点E是∠AOB平分线上的点,EC⊥OA于点C,ED⊥OB于点D,连接CD,求证: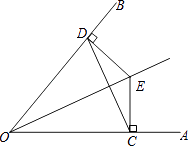
(1)∠ECD=∠EDC;
(2)OE是线段CD的垂直平分线.
【答案】
(1)
解:∵OE是∠AOB的平分线,EC⊥OA,ED⊥OB,
∴EC=ED,
∴∠ECD=∠EDC;
(2)
解:在Rt△ODE和Rt△OCE中,
∵ ![]() ,
,
∴Rt△ODE≌Rt△OCE(HL),
∴OC=OD,
又∵DE=CE,
∴OE是CD的垂直平分线.
【解析】(1)由角平分线的性质即可得证;(2)根据“HL”证Rt△ODE≌Rt△OCE,得OC=OD,由DE=CE可得OE是CD的垂直平分线.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对线段垂直平分线的性质的理解,了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .
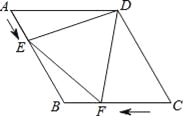
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把两个含有45°角的直角三角板如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.
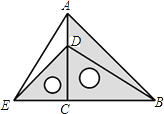
【答案】BF⊥AE,理由详见解析.
【解析】BD=AE ,BD⊥AE.延长BD交AE于F ,证△BCD≌△ACE,可得BD=AE ,BD⊥AE .
∵CE=CD,CA=CB,∠ACE=∠BCD=90°,∴△BCD≌△ACE,∴BD=AE,∠CBD=∠CAE,∵∠CAE+∠AEC=90°,∴∠CBD+∠AEC=90°,∴∠BFE=90°,即BD⊥AE.
【题型】解答题
【结束】
24
【题目】在△ABC中,已知∠B=50°,∠C=60°,AE⊥BC于E,AD平分∠BAC;求:∠DAE的度数.
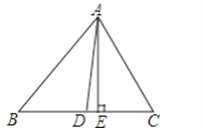
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,直线AB、CD相交于O,OE平分∠BOD,OF平分∠COB,∠2∶∠1=4∶1,求∠AOF的度数.

解:∵OE平分∠BOD
∴∠BOD=__∠1
∵![]() =4
=4
∴∠2=__∠1
∵∠2+∠BOD=____
∴4∠1+2∠1=
∴∠1=30°
∴∠BOD = ;
∴∠AOC= ;
又∵∠BOD+∠BOC=180°
∴∠BOC=120°
∵ OF平分∠COB
∴∠COF=∠BOF= ;
∴∠AOF=60°+60°= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
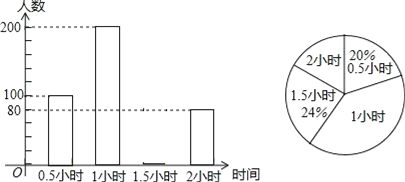
(1)求被抽样调查的学生有多少人?并补全条形统计图;
(2)每天户外活动时间的中位数是 小时?
(3)该校共有1850名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com