
【题目】已知如图,直线AB、CD相交于O,OE平分∠BOD,OF平分∠COB,∠2∶∠1=4∶1,求∠AOF的度数.

解:∵OE平分∠BOD
∴∠BOD=__∠1
∵![]() =4
=4
∴∠2=__∠1
∵∠2+∠BOD=____
∴4∠1+2∠1=
∴∠1=30°
∴∠BOD = ;
∴∠AOC= ;
又∵∠BOD+∠BOC=180°
∴∠BOC=120°
∵ OF平分∠COB
∴∠COF=∠BOF= ;
∴∠AOF=60°+60°= .
【答案】答案见解析
【解析】试题分析:由OE平分∠BOD可得出∠BOD=2∠1,由![]() =4,可得∠2=4∠1,又因为∠2+∠BOD=180°得出4∠1+2∠1=180°,解得∠1=30°,所以∠BOD =∠AOC=60°,
=4,可得∠2=4∠1,又因为∠2+∠BOD=180°得出4∠1+2∠1=180°,解得∠1=30°,所以∠BOD =∠AOC=60°,
进而求出∠BOC=120°,再根据OF平分∠COB可求得∠COF=∠BOF=60,最后计算出∠AOF的度数即可.
试题解析:

解:如图∵OE平分∠BOD,
∴∠BOD=2∠1,
∵![]() =4,
=4,
∴∠2=4∠1,
∵∠2+∠BOD=180°,
∴4∠1+2∠1=180°,
∴∠1=30°,
∴∠BOD =60°;
∴∠AOC=60°;
又∵∠BOD+∠BOC=180°,
∴∠BOC=120°,
∵OF平分∠COB,
∴∠COF=∠BOF=60°,
∴∠AOF=60°+60°=120°.


科目:初中数学 来源: 题型:
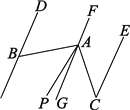
【题目】如图,已知DB∥FG∥EC,A是FG上一点,∠ABD=60°,∠ACE=36°,AP平分∠BAC.
(1)请你求出∠BAC的度数;
(2)请你求出∠PAG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( ) 
A.4.5
B.5
C.5.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是∠AOB平分线上的点,EC⊥OA于点C,ED⊥OB于点D,连接CD,求证: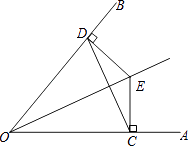
(1)∠ECD=∠EDC;
(2)OE是线段CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形,是因式分解的是( )
A. x(x-1)=x2-x B. x2-x+1 = x(x-1)+1
C. x2-x =" x(x-1)" D. 2a(b+c)=2ab+2ac
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受新型冠状病毒的影响,在2020年3月14日起,我市417所高三初三学校,16.6万学生先后分住校类、部分住校类、走读类分批错时错峰返校,于3月16日正式开学.其中16.6万用科学记数法表示正确的是( )
A.1.66×105B.16.6×105C.1.66×106D.1.66×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com