
【题目】已知,抛物线C1:y=- ![]() x2+mx+m+
x2+mx+m+ ![]()
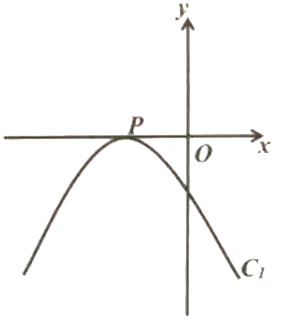
(1)①当m=1时,抛物线与x轴的交点坐标为_______;②当m=2时,抛物线与x轴的交点坐标为________;
(2)①无论m取何值,抛物线经过定点P________;②随着m的取值的变化,顶点M(x,y)随之变化,y是x的函数,记为函数C2 , 则函数C2的关系式为:________;
(3)如图,若抛物线C1与x轴仅有一个公共点时,①直接写出此时抛物线C1的函数关系式;②请在图中画出顶点M满足的函数C2的大致图象,在x轴上任取一点C,过点C作平行于y轴的直线l分别交C1、C2于点A、B,若△PAB为等腰直角三角形,求点C的坐标;
(4)二次函数的图象C2与y轴交于点N,连接PN,若二次函数的图象C1与线段PN有两个交点,直接写出m的取值范围.
【答案】(1)(﹣1,0)(3,0);(﹣1,0)(5,0);(2)(-1,0); y= ![]() (x+1);(3)点C的坐标为(1,0)或(-3,0);(4)-
(x+1);(3)点C的坐标为(1,0)或(-3,0);(4)- ![]() <m≤0
<m≤0
【解析】
(1)①把m=1,y=0分别代入抛物线C1,得到一个一元二次方程,解方程即可求出交点横坐标。其纵坐标都为0;②把①中的m=1改为m=2,方法相同;
(2)把二次函数的C1∴化为顶点式即可求得顶点为:M(m,![]() (m+1)2)∴函数C2的关系式为 y=
(m+1)2)∴函数C2的关系式为 y= ![]() (x+1)2;
(x+1)2;
(3)①当抛物线C1与x轴仅有一个公共点时,即顶点在x轴上,此时M的纵坐标为0,由此可得 则m, 把m代入C1解析式即可;
②分析C1、C2 的解析式可以发现,这两个函数关于x轴对称,可据此画函数的图像;
(4) 若二次函数的图象C1与线段PN有两个交点,则其对称轴与线段PN一定有交点,据此即可求出答案。
(1)①把m=1,y=0分别代入抛物线C1,得到一个一元二次方程,解方程即可求出交点横坐标。其纵坐标都为0;②把①中的m=1改为m=2,方法相同;
(2)把二次函数的C1∴化为顶点式即可求得顶点为:M(m,![]() (m+1)2)∴函数C2的关系式为 y=
(m+1)2)∴函数C2的关系式为 y= ![]() (x+1)2;
(x+1)2;
(3)解:如图所示,

∵抛物线C1:y=- ![]() x2+mx+m+
x2+mx+m+ ![]() 顶点在x轴,则m=-1,
顶点在x轴,则m=-1,
∴抛物线C1:y=- ![]() x2-x-
x2-x- ![]() =-
=- ![]() (x+1)2 , P(-1,0),由②知,函数C2的关系式为y=
(x+1)2 , P(-1,0),由②知,函数C2的关系式为y= ![]() (x+1)2;∴抛物线C1与C2关于x轴对称,∵△PAB为等腰直角三角形,∴直角顶点只能是点P , 且PC=BC=AC , 设B(n ,
(x+1)2;∴抛物线C1与C2关于x轴对称,∵△PAB为等腰直角三角形,∴直角顶点只能是点P , 且PC=BC=AC , 设B(n , ![]() (n+1)2),∴C(n , 0),BC=
(n+1)2),∴C(n , 0),BC= ![]() (n+1)2 , ∴PC=|n+1|,∴
(n+1)2 , ∴PC=|n+1|,∴ ![]() (n+1)2=|n+1|,∴n=-1(舍)或n=1或n=-3.∴点C的坐标为(1,0)或(-3,0)
(n+1)2=|n+1|,∴n=-1(舍)或n=1或n=-3.∴点C的坐标为(1,0)或(-3,0)
(4)解:- ![]() <m≤0
<m≤0
解:(1)①(﹣1,0)(3,0);②(﹣1,0)(5,0);(2)①∵抛物线C1:y=- ![]() x2+mx+m+
x2+mx+m+ ![]() =-
=- ![]() x2+m(x+1)+
x2+m(x+1)+ ![]() .
.
∴当x+1=0时,无论m为何值,抛物线经过定点P , ∴x=-1,y=0,∴定点P(-1,0),故答案为:-1,0;
②抛物线C1:y=- ![]() x2+mx+m+
x2+mx+m+ ![]() =-
=- ![]() (x-m)2+
(x-m)2+ ![]() (m+1)2 .
(m+1)2 .
∴M(m,![]() (m+1)2),∴函数C2的关系式为y=
(m+1)2),∴函数C2的关系式为y= ![]() (x+1)2;故答案为:y=
(x+1)2;故答案为:y= ![]() (x+1)2
(x+1)2


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
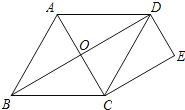
【题目】如图,菱形ABCD的对角线交于点O,点E是菱形外一点,DE∥AC,CE∥BD.
(1)求证:四边形DECO是矩形;
(2)连接AE交BD于点F,当∠ADB=30°,DE=2时,求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
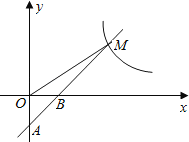
【题目】如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数![]() 的图象在第一象限内的交点为M,若△OBM的面积为2.
的图象在第一象限内的交点为M,若△OBM的面积为2.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(1,5)和点B,与y轴相交于点C(0,6).
的图象相交于点A(1,5)和点B,与y轴相交于点C(0,6).
(1)求一次函数和反比例函数的解析式;
(2)现有一直线l与直线y=kx+b平行,且与反比例函数y=![]() 的图象在第一象限有且只有一个交点,求直线l的函数解析式.
的图象在第一象限有且只有一个交点,求直线l的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
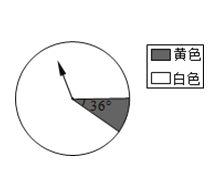
【题目】某厂为新型号电视机上市举办促销活动,顾客每买一台该型号电视机,可获得一次抽奖机会,该厂拟按10%设大奖,其余90%为小奖。广家设计的抽奖方案是:在一个不透明的盒子中,放入10个黄球和90个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球的顾客获得大奖,摸到白球的顾客获得小奖。
(1)厂家请教了一位数学老师,他设计的抽奖方案是:在一个不透明的盒子中,放入2个黄球和3个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球的顾客获得大奖,其余的顾客获得小奖。该抽奖方案符合厂家的设奖要求吗?请说明理由;
(2)下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上黄、白两种颜色,并设计抽奖方案,使其符合厂家的设奖要求。(友情提醒:1.转盘上用文字注明颜色和扇形的圆心角的度数;2.结合转盘简述获奖方式,不需说明理由.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为__________
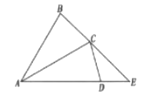
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与直线
与直线![]() 有两个不同的交点,其中一个交点在线段
有两个不同的交点,其中一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),另一个交点在线段
两个端点),另一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),则
两个端点),则![]() 的取值范围是
的取值范围是
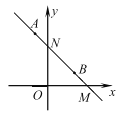
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O为△ABC(∠A<∠ABC)的外接圆,且AB为![]() 的直径,AB=8,点D为AB延长线上一点,点 E为半径OB上一点,连接CD、CE、OC,且∠BCD=∠A.
的直径,AB=8,点D为AB延长线上一点,点 E为半径OB上一点,连接CD、CE、OC,且∠BCD=∠A.

(1)求证:CD为![]() 的切线;
的切线;
(2)若CB=CE,求证:CE2=CO2-OA·OE;
(3)在(2)的条件下,求OE+BC的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com