
【题目】某学校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
【答案】
(1)
解:设A种树每棵x元,B种树每棵y元,依题意得:
![]() ,
,
解得 ![]() .
.
答:A种树每棵100元,B种树每棵80元;
(2)
解:设购买A种树木为a棵,则购买B种树木为(100﹣a)棵,依题意得:
a≥3(100﹣a),
解得a≥75.
设实际付款总金额是y元,则
y=0.9[100a+80(100﹣a)],
即y=18a+7200.
∵18>0,y随a的增大而增大,
∴当a=75时,y最小.
即当a=75时,y最小值=18×75+7200=8550(元).
答:当购买A种树木75棵,B种树木25棵时,所需费用最少,最少为8550元.
【解析】(1)设A种树每棵x元,B种树每棵y元,根据“购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元”列出方程组并解答;(2)设购买A种树木为a棵,则购买B种树木为(100﹣a)棵,根据“购买A种树木的数量不少于B种树木数量的3倍”列出不等式并求得a的取值范围,结合实际付款总金额=0.9(A种树的金额+B种树的金额)进行解答.


科目:初中数学 来源: 题型:
【题目】图①、②、③均是4×4的正方形网格,每个小正方形顶点叫做格点,点O和线段AB的端点在格点上,按要求完成下列作图.
(1)在图①、②中分别找到格点C、D,使以点A、B、C、D为顶点的四边形是平行四边形,且点O到这个四边形的两个端点的距离相等,画出两个这样的平行四边形.
(2)在图③中找到格点E、F,使以A、B、E、F为顶点的四边形的面积最大,且点O到这个四边形的两个端点的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,BC=8,以C为圆心适当长为半径画弧分别交BC,CD于M,N两点,分别以M,N为圆心,以大于 ![]() MN的长为半径画弧,两弧在∠BCD的内部交于点P,连接CP并延长交AD于E,交BA的延长线于F,则AE+AF的值等于 .
MN的长为半径画弧,两弧在∠BCD的内部交于点P,连接CP并延长交AD于E,交BA的延长线于F,则AE+AF的值等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在圆心角为90°的扇形AOB中,半径OA=3,OC=AC,OD= ![]() BD,F是弧AB的中点.将△OCD沿CD折叠,点O落在点E处,则图中阴影部分的面积为 .
BD,F是弧AB的中点.将△OCD沿CD折叠,点O落在点E处,则图中阴影部分的面积为 . 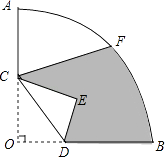
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图: 第一步,分别以点A、D为圆心,以大于 ![]() AD的长为半径在AD两侧作弧,交于两点M、N;
AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( )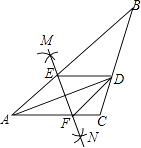
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
训练后篮球定时定点投篮测试进球数统计表
请你根据图表中的信息回答下列问题:
(1)选择长跑训练的人数占全班人数的百分比为 , 该班学生的总人数为;
(2)训练后篮球定时定点投篮人均进球数为;
(3)若将选择篮球的同学的进球数写在外观、大小一样的枝条上,放在不透明的盒子中,搅拌均匀后,从中抽取一张,则抽到4的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,Rt△ABC中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点. 
(1)求证DA是⊙O的切线;
(2)DP的长度为多少时,∠BPC的度数最大,最大度数是多少?请说明理由.
(3)P运动的过程中,(PB+PC)的值能否达到最小,若能,求出这个最小值,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
社会消费品零售总额是指批发和零售业,住宿和餐饮业以及其他行业直接售给城乡居民和社会集团的消费品零售额,在各类与消费有关的统计数据中,社会消费品零售总额是表现国内消费需求最直接的数据.
2012年,北京市全年实现社会消费品零售总额7702.8亿元,比上一年增长11.6%,2013年,全年实现社会消费品零售总额8375.1亿元,比上一年增长8.7%,2014年,全年实现社会消费品零售总额9098.1亿元,比上一年增长8.6%,2015年,全年实现社会消费品零售总额10338亿元,比上一年增长7.3%.
2016年,北京市实现市场总消费19926.2亿元,比上一年增长了8.1%,其中实现服务性消费8921.1亿元,增长10.1%;实现社会消费品零售总额11005.1亿元,比上一年增长了6.5%.
根据以上材料解答下列问题:
(1)补全统计表:
2012﹣2016年北京市社会消费品零售总额统计表
年份 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 |
社会消费品零售总额(单位:亿元) |
(2)选择适当的统计图将2012﹣2016年北京市社会消费品零售总额比上一年的增长率表示出来,并在图中表明相应数据;
(3)根据以上信息,估计2017年北京市社会消费品零售总额比上一年的增长率约为 , 你的预估理由是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com