
 解:(1)把(-3,0)(1,0)(0,3)代入y=ax2+bx+c可得
解:(1)把(-3,0)(1,0)(0,3)代入y=ax2+bx+c可得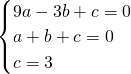 ,
,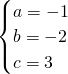 ,
, ,BD=2
,BD=2 ,
, ,
, ,
, ,
, .
. .
. ,
, ,
, .
. .
. ,
,

 ,
, ;
; 消去y,得x2+x+m=0.
消去y,得x2+x+m=0.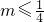 .
.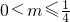 .
. 个单位长度.
个单位长度. 个单位长度.
个单位长度. ,解可求DH,进而可求BH、CH,由于∠PBA=∠CBD,易证Rt△FBO∽Rt△CBH,
,解可求DH,进而可求BH、CH,由于∠PBA=∠CBD,易证Rt△FBO∽Rt△CBH,

 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
 已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.
已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
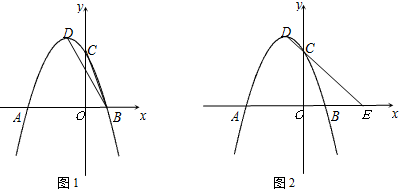
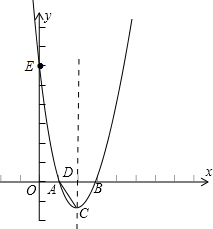
 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,将抛物线y=-
如图,将抛物线y=-| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com