
����Ŀ��������ijˮ����ֳ������С��Ϻ��ֳ����֪ÿǧ��С��Ϻ��ֳ�ɱ�Ϊ6Ԫ������������������80������۵���p��Ԫ/ǧ�ˣ���ʱ���t���죩֮��ĺ�����ϵΪ��![]() ��1��t��80��tΪ����������������y��ǧ�ˣ���ʱ���t���죩֮��ĺ�����ϵ��ͼ��ʾ��
��1��t��80��tΪ����������������y��ǧ�ˣ���ʱ���t���죩֮��ĺ�����ϵ��ͼ��ʾ��
��1������������y��ʱ��t�ĺ�����ϵʽ��
��2����һ������������������������Ƕ��٣�
��3����ʵ�����۵�ǰ40���У�����ֳ������ÿ����1ǧ��С��Ϻ���;���m��m��7��Ԫ�������������������ǰ40���У�ÿ��۳��������������������ʱ��t�������������m��ȡֵ��Χ��
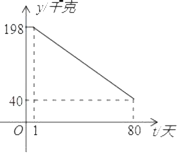
���𰸡���1��y��2t��200��1��t��80��tΪ����������2����30�������������������������2450Ԫ����3��5��m��7��
��������
��1�����ݺ���ͼ�����ô���ϵ������⼴�ɣ�
��2��������������ΪW�������������������ۼ��ɱ����������������г���������ʽ���ɶ��κ��������������ֵ�����жϣ�
��3��������������ΪW�������������������ۼ��ɱ����������������г���������ʽ�����ö��κ��������ʽ��ǰ40��ÿ��۳��������������������ʱ��t��������������ɵã�
�⣺��1���躯����ϵʽΪy��kt��b��k��0����
����1��198������80��40�����룬�ã�![]() ��
��
��ã�![]() ��
��
����������y��ʱ��t�ĺ�����ϵʽΪ��y��2t��200��1��t��80��tΪ��������
��2��������������ΪW��
��![]() ��
��
��![]() ��
��
�൱t=30ʱ��W�����2450��
�𣺵�30�������������������������2450Ԫ��
��3��������������ΪW��
��������ã�![]() ��
��
�亯��ͼ��ĶԳ���Ϊt��2m��30��
�ߵ�1��t��40ʱ��W��t�����������
���ɶ��κ�����ͼ�������ʿ�֪2m��30��40��
��ã�m��5��
�֡�m��7��
��5��m��7��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��![]() �ֱ���x�ᡢy���ཻ���M��N���߳�Ϊ2��������OABCһ������O������ϵ��ԭ�㣬ֱ��AN��MC�ཻ���P�������������ŵ�O��תһ�ܣ����P���㣨0��2�����ȵ���Сֵ�ǣ� ��
�ֱ���x�ᡢy���ཻ���M��N���߳�Ϊ2��������OABCһ������O������ϵ��ԭ�㣬ֱ��AN��MC�ཻ���P�������������ŵ�O��תһ�ܣ����P���㣨0��2�����ȵ���Сֵ�ǣ� ��
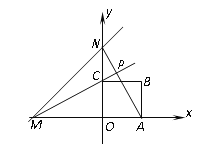
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�麬30��������CAB��30�����ǵ����ǰ��һ��������ƴ��һ�����ǰ�б��AB������������Բ��ֱ��MN�غϣ�������������Ե�Ķ����Ǵ�N�㿪ʼ����N��Ķ���Ϊ0������������CP���ŵ�C��CA˳ʱ����ÿ��2�ȵ��ٶ���ת������ACB���Բ����Ϊֹ������ת�����У�����CP���������İ�Բ������E��
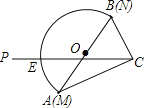
��1��������CP����ABC�����Բ����ʱ��������CP��ת�����Ƕ��٣�
��2��������CP�ֱ���ABC�����ġ�����ʱ����E���Ķ����ֱ��Ƕ��٣�
��3������ת7.5��ʱ������BE����֤��BE��CE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x1��x2�ǹ���x�ķ���x2+��3k+1��x+2k2+1��0�����������ʵ�����������㣨x1��1����x2��1����8k2����k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��
��
��1���ö��κ���ͼ����x��Ľ���������______________��
��2����![]() ����
����![]() ����ʽ_____________________����д����������______________��
����ʽ_____________________����д����������______________��
��3�����������л����������ߵĴ���ͼ��
��4��д������ʽ![]() �Ľ⼯___________________��
�Ľ⼯___________________��
��5����![]() ʱ��ֱ��д��y��ȡֵ��Χ_________________��
ʱ��ֱ��д��y��ȡֵ��Χ_________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��һ�㣬
��һ�㣬![]() ��
��![]() ��
��![]() ����һ���㣬���ı���
����һ���㣬���ı���![]() ��ֱ��
��ֱ��![]() �۵���
�۵���![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ����
����![]() �ij�����Сʱ����
�ij�����Сʱ����![]() �ij�Ϊ_______
�ij�Ϊ_______
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͨѶ��˾�涨��һ���ͻ����һ���µ�ͨ��ʱ�䲻����![]() ���ӣ���ô����������ͻ�ֻҪ��10Ԫͨ���ѣ��������
���ӣ���ô����������ͻ�ֻҪ��10Ԫͨ���ѣ��������![]() ���ӣ���ô����³�����Ҫ��10Ԫͨ�����⣬�������ֻ�Ҫ��ÿ����
���ӣ���ô����³�����Ҫ��10Ԫͨ�����⣬�������ֻ�Ҫ��ÿ����![]() Ԫ���ѣ�
Ԫ���ѣ�
����ij���ͻ�7�·�ͨ��90���ӣ������˹涨��![]() ���ӣ�������Ӧ��ͨ����______Ԫ���ú�
���ӣ�������Ӧ��ͨ����______Ԫ���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
�����±���ʾij���ͻ�8�·ݡ�9�·ݵ�ͨ������ͽ��������
�·� | ͨ��ʱ��/���� | ͨ��������/Ԫ |
8�·� | 80 | 25 |
9�·� | 45 | 10 |
�����ϱ������ݣ���![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������
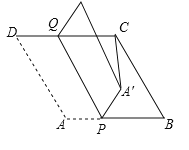
��1����ͼ1����֪��ACB����ADB��90�������ó߹���ͼ������ABD�����Բ��������ͼ�ۼ�����д����������C�Ƿ�����ABD�����Բ���� ����������������������
����̽��
��2����ͼ2���ı���ADBC�ǡ�O���ڽ��ı��Σ���ACB����ADB��90����AD��BD����֤��CA+CB��![]() CD��
CD��
��3����ͼ3����P��������ABCD�Խ���AC���е㣬��E��ƽ����һ�㣬EB��AB��EA��![]() BA����Q���߶�AE���е㣬����ͼ�л�����E�������߶�PQ��AB֮���������ϵ��
BA����Q���߶�AE���е㣬����ͼ�л�����E�������߶�PQ��AB֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�У�![]() ��
��![]() ����ABC��75����BC��2����ͼ����Ӱ���ֵ�����ǣ� ��.
����ABC��75����BC��2����ͼ����Ӱ���ֵ�����ǣ� ��.

A.2��![]() B.2��
B.2��![]() C.4��
C.4��![]() D.
D.![]() ��
��![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com