
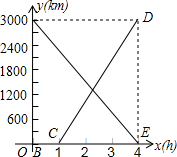
 A、B两机场相距3000km,甲、乙两架飞机沿同一航线分别从A、B两机场出发相向而行,假设它们都保持匀速行驶,如图,线段AE、CD分别表示甲、乙两机离B机场的距离y(km)和所用去的时间x(h)之间的函数关系的图象,观察图象回答下列问题:
A、B两机场相距3000km,甲、乙两架飞机沿同一航线分别从A、B两机场出发相向而行,假设它们都保持匀速行驶,如图,线段AE、CD分别表示甲、乙两机离B机场的距离y(km)和所用去的时间x(h)之间的函数关系的图象,观察图象回答下列问题:分析 (1)由图中可明显看出,乙比甲少用一小时.通过两地距离及所用时间求出甲乙两机速度;
(2)通过设出函数一般表达式,将坐标代入求出函数关系式;
(3)两函数图象交点的横坐标即为相遇时的时间,将两函数联立求得相遇时间,及相遇时离A机场的距离.
解答 解:(1)由图中可看出,乙机在甲机出发后1小时才从玉树机场出发.甲机飞行速度v1=$\frac{3000}{4}$=750千米/时,乙机飞行速度
v2=$\frac{3000}{3}$=1000千米/时;
(2)甲机y与x的函数关系式y=-750x+3000,
乙机y与x的函数关系式y=1000x-1000;
(3)由图可知:
-750x+3000=1000x-1000,
解得:x=$\frac{16}{7}$,
则乙飞行的时间x-1=$\frac{9}{7}$,
把x=$\frac{16}{7}$代入y=-750x+3000得:y=-750×$\frac{16}{7}$+3000=$\frac{9000}{7}$,
所以此时距离A机场3000-$\frac{9000}{7}$=$\frac{12000}{7}$≈1714km.
点评 本题主要考查了函数图象与实际相结合的问题,旨在培养运用函数方程解决实际问题的能力.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com